Reuleaux triangle

A Reuleaux triangle is, apart from the trivial case of the circle, the simplest and best known Reuleaux polygon, a curve of constant width. The separation of two parallel lines tangent to the curve is independent of their orientation. The term derives from Franz Reuleaux, a 19th-century German engineer who did pioneering work on ways that machines translate one type of motion into another, although the concept was known before his time.

Contents 1 Construction 2 Reuleaux polygons 3 Other uses 4 Three-dimensional version 5 See also 6 Notes 7 External links

Construction

With a compass, sweep an arc sufficient to enclose the desired figure. With radius unchanged, sweep a sufficient arc centred at a point on the first arc to intersect that arc. With the same radius and the centre at that intersection sweep a third arc to intersect the other arcs. The result is a curve of constant width. Because all diameters are the same, the Reuleaux triangle is an answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

Equivalently, given an equilateral triangle T of side length s, take the boundary of the intersection of the disks with radius s centered at the vertices of T.

By the Blaschke-Lebesgue theorem, the Reuleaux triangle has the least area of any curve of given constant width. This area is 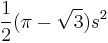, where s is the constant width. The existence of Reuleaux polygons shows that diameter measurements alone cannot verify that an object has a circular cross-section.

The area of Reuleaux triangle is smaller than that of the disk of the same width (ie diameter); the area of such a disk is .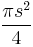

Reuleaux polygons

The Reuleaux triangle can be generalized to regular polygons with an odd number of sides, yielding a Reuleaux polygon. The most commonly used of these is the Reuleaux heptagon, which is the shape of several coins:

• British twenty pence and fifty pence.
• Botswana pula coins in the denominations of 2 Pula, 1 Pula, 25 Thebe and 5 Thebe.
• Cypriot 50 cent coin, from 1991 until Cyprus joined the Euro in 2008.

The constant width of such coins allows their use in coin-operated machines.

Other uses

• The rotor of the Wankel engine is easily mistaken for a Reuleaux triangle but its curved sides are somewhat flatter than those of a Reuleaux triangle and so it does not have constant width.^[1]

• The Harry Watt square drill bit has the shape of a Reuleaux triangle and can, if mounted in a special chuck which allows for the bit not having a fixed centre of rotation, drill a hole that is nearly square.^[2] The Harry Watt square is often used in mortising^[3][4] Other Reuleaux polygons are used to drill pentagonal, hexagonal, and octagonal holes.

• A Reuleaux triangle (along with all other curves of constant width) can roll but makes a poor wheel because it does not roll about a fixed center of rotation. An object on top of rollers with cross-sections that were Reuleaux triangles would roll smoothly and flatly, but an axle attached to Reuleaux triangle wheels would bounce up and down three times per revolution. This concept was used in a science fiction short story by Poul Anderson titled "The Three-Cornered Wheel."

• Several pencils are manufactured in this shape, rather than the more traditional round or hexagonal barrels.^[5] They are usually promoted as being more comfortable or encouraging proper grip, as well as being less likely to roll off tables.

• The shape is used for signage for the National Trails System administered by the United States National Park Service,^[6] as well as the logo of Colorado School of Mines.

• Valve covers used in the Mission Bay Project of San Francisco to differentiate reclaimed water from potable water are in the shape of a Reuleaux triangle.^[7]

Three-dimensional version

The intersection of four spheres of radius s centered at the vertices of a regular tetrahedron with side length s is called the Reuleaux tetrahedron, but is not a surface of constant width.^[8] It can, however, be made into a surface of constant width, called Meissner's tetrahedron, by replacing its edge arcs by curved surface patches. Alternatively, the surface of revolution of a Reuleaux triangle through one of its symmetry axes forms a surface of constant width, with minimum volume among all known surfaces of revolution of given constant width (Campi, Colesanti & Gronchi (1996)).

See also

• Deltoid curve
• Superellipse
• Vesica piscis
• Watts Brothers Tool Works

Notes

• Heinrich Guggenheimer (1977) Applicable Geometry, page 58, Krieger, Huntington ISBN 0882753681 .

External links

• How Round is Your Circle? - book about various geometric properties, including curves and solids of constant width
• Shapes of constant width at cut-the-knot