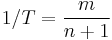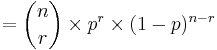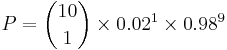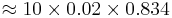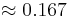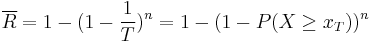Return period
A return period also known as a recurrence interval is an estimate of the interval of time between events like an earthquake, flood or river discharge flow of a certain intensity or size. It is a statistical measurement denoting the average recurrence interval over an extended period of time, and is usually required for risk analysis (i.e. whether a project should be allowed to go forward in a zone of a certain risk) and also to dimension structures so that they are capable of withstanding an event of a certain return period (with its associated intensity).
Contents |
Equation
Recurrence interval = 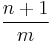
- n is number of years on record;
- m is the rank of the event being considered
For floods, this is conventionally measured in terms of m³/s; for storm surges, in terms of the height of the surge, and similarly for other events.
Return period as "expected frequency"
The theoretical return period is the inverse of the probability that the event will be exceeded in any one year. For example, a 10-year flood has a 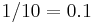 or 10% chance of being exceeded in any one year and a 50-year flood has a 0.02 or 2% chance of being exceeded in any one year.
or 10% chance of being exceeded in any one year and a 50-year flood has a 0.02 or 2% chance of being exceeded in any one year.
While it is true that a 10-year event will occur, on average, once every 10 years and that a 100-year event is so large that we expect it only to occur every 100 years, this is only a statistical statement: the expected number of 100-year events in an n year period is n/100, in the sense of expected value. Similarly, the expected time until another 100-year event is 100 years, and if in a given year or years the event does not occur, the expected time until it occurs remains 100 years, with this "100 years" resetting each time.
It does not mean that 100-year floods will happen regularly, every 100 years, despite the connotations of the name "return period": in any given 100-year period, a 100-year storm may occur once, twice, more, or not at all, and each outcome has a probability that can be computed as below.
Note also that the estimated return period below is a statistic: it is computed from a set of data (the observations), as distinct from the theoretical value in an idealized distribution. One does not actually know that a certain magnitude or greater happens with 1% probability, only that it has been observed exactly once in 100 years.
This distinction is significant because there are few observations of rare events: for instance if observations go back 400 years, the most extreme event (a 400-year event by the statistical definition) may later be classed, on longer observation, as a 200-year event (if a comparable event immediately occurs) or a 500-year event (if no comparable event occurs for 100 years).
Further, one cannot determine the size of a 1,000-year event based on such records alone, but instead must use a statistical model to predict the magnitude of such an (unobserved) event.
Probability distribution
In a given period of n years, the probability of a given number k of events of a given return interval T is given by the binomial distribution as follows. In the limit of long periods (as n grows large), this converges to the Poisson distribution.
Take
where
- T is return interval
- m is ranking
- n is number of occurrences
If the probability of an event occurring is p, then the probability of the event not occurring is 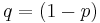 . The binomial distribution can be used to find the probability of occurrence of an event r times in a period of n years.
. The binomial distribution can be used to find the probability of occurrence of an event r times in a period of n years.
Example
Given that the return period of an event is 50 years,
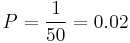 .
.
So the probability that such an event occurs exactly once in 10 successive years is;
Risk analysis
Return period is also useful for risk analysis (such as natural, inherent, or hydrologic risk of failure).[1] When dealing with a structure design expectations the return period is useful in calculating the risk of the structure with respect to a given storm return period when given the design life expectation.
This is the likelihood of at least one event that exceeds design limits during the expected life of the structure: it is the complement of the likelihood that no events exceed design limits.
The equation for assessing this risk can be expressed as
where
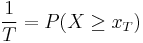 is the expression for the probability of the occurrence for the hydrologic event in question;
is the expression for the probability of the occurrence for the hydrologic event in question;- n is the expected life of the structure.
See also
References
- ^ Water Resources Engineering, 2005 Edition, John Wiley & Sons, Inc, 2005.
External links
- CumFreq, a computer program for cumulative frequencies, return periods, and confidence intervals