Resilience

Resilience is the property of a material to absorb energy when it is deformed elastically and then, upon unloading to have this energy recovered. In other words, it is the maximum energy per unit volume that can be elastically stored. It is represented by the area (integral) under the curve in the elastic region (the initial, linear portion) of the stress-strain curve; this quantity is also known as the elastic potential energy of a material.

The modulus of resilience is defined as the energy that can be absorbed per unit volume without creating a permanent distortion. It can be calculated by integrating the stress-strain curve from zero to the elastic limit.

Modulus of resilience, 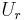$U_r$ , can be calculated using the following formula: 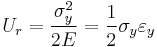$U_r=\frac{\sigma_y^2}{2E}=\frac{1}{2} \sigma_y \varepsilon_y$ , where 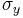$\sigma_y$ is yield stress, $E$ is Young's modulus, and 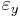$\varepsilon_y$ is the strain at the yield stress.^[1]

An example of a biomaterial which has a high resilience is articular cartilage, the substance lining the ends of bones in articulating joints such as the knee and hip.

It might be different from rebound resilience, which is used for instance in relation with foam.

The maximum energy which can be stored in a body up to elastic limit is called proof resilience.

References

^ From: Eugene A. Avallone, et al. eds. Marks' Standard Handbook for Mechanical Engineers, 11th ed., 2007