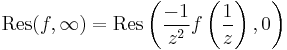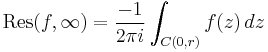Residue at infinity

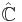In complex analysis a branch of mathematics, the residue at infinity is a residue of a holomorphic function on an annulus having an infinite external radius. The infinity $\infty$ is a point added to the local space $\mathbb C$ in order to render it compact (in this case it is a one-point compactification). This space noted $\hat{\mathbb C}$ is isomorphic to the Riemann sphere.^[1] One can use the residue at infinity to calculate some integrals.

Definition

Given a holomorphic function f on an annulus 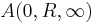$A(0, R, \infty)$ (centered at 0, with inner radius $R$ and infinite outer radius), the residue at infinity of the function f can be defined in terms of the usual residue as follows:

$\mathrm{Res}(f,\infty) = \mathrm{Res}\left( {-1\over z^2}f\left({1\over z}\right), 0 \right)$

Thus, one can transfer the study of 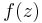$f(z)$ at infinity to the study of 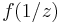$f(1/z)$ at the origin.

Note that 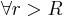$\forall r > R$ , we have

$\mathrm{Res}(f, \infty) = {-1\over 2\pi i}\int_{C(0, r)} f(z) \, dz$

References

This article incorporates information from this version of the equivalent article on the French Wikipedia.

^ Michèle AUDIN, Analyse Complexe, cursus notes of the university of Strasbourg available on the web, pp. 70–72

Murray R. Spiegel, Variables complexes, Schaum, ISBN 2-7042-0020-3
Henri Cartan, Théorie analytique des fonctions d'une ou plusieurs varaiables complexes, Hermann, 1961

Residue at infinity

Definition

See also

References