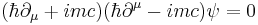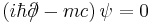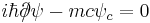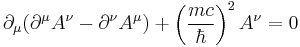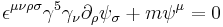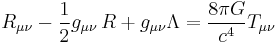Relativistic wave equations

Before the creation of quantum field theory, physicists attempted to formulate versions of the Schrödinger equation which were compatible with special relativity. Such equations are called relativistic wave equations.

The first such equation was discovered by Erwin Schrödinger himself; however, he realized that this equation, now called the Klein-Gordon equation, gave incorrect results when used to calculate the energy levels of hydrogen. Schrödinger discarded his relativistic wave equation, only to realize a few months later that its non-relativistic limit (what is now called the Schrödinger equation) was still of importance.

1 List of relativistic wave equations
2 See also

List of relativistic wave equations

The following list of relativistic wave equations is categorised by the spin of the particles they describe.

Spin 0

Klein-Gordon equation: describes a massless or massive spin-0 particle (such as Higgs bosons)

$(\hbar \partial_{\mu} %2B imc)(\hbar \partial^{\mu} -imc)\psi = 0$

Spin 1/2

Weyl equation: describes massless spin-1/2 particles
Dirac equation: describes massive spin-1/2 particles (such as electrons)

$\left( i \hbar \partial\!\!\!/ - m c \right) \psi = 0$

Majorana equation: describes a massive Majorana particle

$i \hbar \partial\!\!\!/ \psi - m c \psi_c = 0$

Breit equation: describes two massive spin-1/2 particles (such as electrons) interacting electromagnetically to first order in perturbation theory

Spin 1

Maxwell equations: describe a photon (massless spin-1 particle)
Proca equation: describes a massive spin-1 particle (such as W and Z bosons)

$\partial_\mu(\partial^\mu A^\nu - \partial^\nu A^\mu)%2B\left(\frac{mc}{\hbar}\right)^2 A^\nu=0$

Gauge fields

Yang-Mills equation: describes a non-abelian gauge field
Yang–Mills–Higgs equations: describes a non-abelian gauge field coupled with a massive spin-0 particle
Kemmer equation: an alternative equation for spin-0 and spin-1 particles

Spin 3/2

Rarita-Schwinger equation: describes a massive spin-3/2 particle

$\epsilon^{\mu \nu \rho \sigma} \gamma^5 \gamma_\nu \partial_\rho \psi_\sigma %2B m\psi^\mu = 0$

Spin 2

Einstein field equations: describe interaction of matter with the gravitational field (massless spin-2 field).

$R_{\mu \nu} - {1 \over 2}g_{\mu \nu}\,R %2B g_{\mu \nu} \Lambda = {8 \pi G \over c^4} T_{\mu \nu}$

Arbitrary spin

Bargmann-Wigner equations: describe free particles of arbitrary integral or half-integral spin

All the particle equations except the Breit, the Yang–Mills, Yang–Mills–Higgs and Einstein are linear.