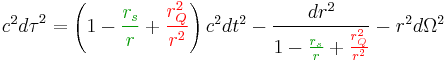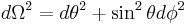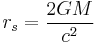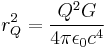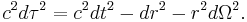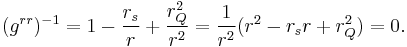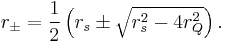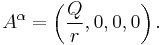Reissner–Nordström metric
| General relativity |
|---|
| Introduction Mathematical formulation Resources |
|
Fundamental concepts
|
|
Phenomena
|
|
Advanced theories
|
|
Schwarzschild
Reissner–Nordström · Gödel Kerr · Kerr–Newman Kasner · Taub-NUT · Milne · Robertson–Walker pp-wave · van Stockum dust |
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein-Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M.
Contents |
The metric
Discovered by Hans Reissner and Gunnar Nordström, their metric can be written as
where
- τ is the proper time (time measured by a clock moving with the particle) in seconds,
- c is the speed of light in meters per second,
- t is the time coordinate (measured by a stationary clock at infinity) in seconds,
- r is the radial coordinate (circumference of a circle centered on the star divided by 2π) in meters,
- Ω is the solid angle,
-
- rs is the Schwarzschild radius (in meters) of the massive body, which is related to its mass M by
-
- where G is the gravitational constant, and
- rQ is a length-scale corresponding to the electric charge Q of the mass
-
- where 1/4πε0 is Coulomb's force constant.[1]
The colors have been added in order to highlight the extensions to Minkowski spacetime. In the limit that the charge Q (or equivalently, the length-scale rQ) goes to zero, one recovers the Schwarzschild metric. To do this, you just remove term in  . The classical Newtonian theory of gravity may then be recovered in the limit as the ratio rs/r goes to zero. To do this, you just remove term in
. The classical Newtonian theory of gravity may then be recovered in the limit as the ratio rs/r goes to zero. To do this, you just remove term in  . In that limit, the metric returns to the Minkowski metric for special relativity
. In that limit, the metric returns to the Minkowski metric for special relativity
In practice, the ratio rs/r is almost always extremely small. For example, the Schwarzschild radius rs of the Earth is roughly 9 mm (³⁄8 inch), whereas a satellite in a geosynchronous orbit has a radius r that is roughly four billion times larger, at 42,164 km (26,200 miles). Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The ratio only becomes large close to black holes and other ultra-dense objects such as neutron stars.
Charged black holes
Although charged black holes with  are similar to the Schwarzschild black hole, they have two horizons: the event horizon and an internal Cauchy horizon. As usual, the event horizons for the spacetime are located where
are similar to the Schwarzschild black hole, they have two horizons: the event horizon and an internal Cauchy horizon. As usual, the event horizons for the spacetime are located where 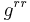 diverges:
diverges:
The second factor r 2 − rs r + rQ2 is a quadratic in r and we find its zeros by using the quadratic formula:
These concentric event horizons become degenerate for 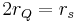 which corresponds to an extremal black hole. Black holes with
which corresponds to an extremal black hole. Black holes with 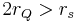 are believed not to exist in nature because they would contain a naked singularity; their appearance would contradict Roger Penrose's cosmic censorship hypothesis which is generally believed to be true. Theories with supersymmetry usually guarantee that such "superextremal" black holes can't exist.
are believed not to exist in nature because they would contain a naked singularity; their appearance would contradict Roger Penrose's cosmic censorship hypothesis which is generally believed to be true. Theories with supersymmetry usually guarantee that such "superextremal" black holes can't exist.
The electromagnetic potential is
If magnetic monopoles are included into the theory, then a generalization to include magnetic charge  is obtained by replacing
is obtained by replacing 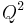 by
by 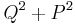 in the metric and including the term
in the metric and including the term 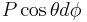 in the electromagnetic potential.
in the electromagnetic potential.
See also
Notes
- ^ Landau 1975.
References
- Reissner, H (1916). "Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie". Annalen der Physik 50: 106–120. Bibcode 1916AnP...355..106R. doi:10.1002/andp.19163550905.
- Nordström, G (1918). "On the Energy of the Gravitational Field in Einstein's Theory". Verhandl. Koninkl. Ned. Akad. Wetenschap., Afdel. Natuurk., Amsterdam 26: 1201–1208.
- Adler, R; Bazin M, and Schiffer M (1965). Introduction to General Relativity. New York: McGraw-Hill Book Company. pp. 395–401. ISBN 978-0-07-000420-7.
- Wald, RM (1984). General Relativity. Chicago: The University of Chicago Press. pp. 158, 312–324. ISBN 978-0-226-87032-8.
External links
- spacetime diagrams including Finkelstein diagram and Penrose diagram, by Andrew J. S. Hamilton
- "Particle Moving Around Two Extreme Black Holes" by Enrique Zeleny, The Wolfram Demonstrations Project.
|
||||||||||||||||||||||||||||