Reinhardt cardinal
In set theory, a branch of mathematics, a Reinhardt cardinal is a large cardinal κ, suggested by William Nelson Reinhardt (1967, 1974), that is the critical point of a non-trivial elementary embedding j of V into itself.
A minor technical problem is that this property cannot be formulated in the usual set theory ZFC: the embedding j is a class of the form 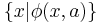 for some set a and formula φ, and in the language of set theory it is not possible to quantify over all classes (or formulas). There are several ways to get round this. One way is to add a new function symbol j to the language of ZFC, together with axioms stating that j is an elementary embedding of V (and of course adding separation and replacement axioms for formulas involving j). Another way is to use a class theory such as NBG or KM. A third way is to treat Kunen's theorem as a countable infinite collection of theorems, one for each formula φ. (It is possible to have elementary embeddings of models of ZFC into themselves assuming a mild large cardinal hypothesis, but these elementary embeddings are not classes of the model.)
for some set a and formula φ, and in the language of set theory it is not possible to quantify over all classes (or formulas). There are several ways to get round this. One way is to add a new function symbol j to the language of ZFC, together with axioms stating that j is an elementary embedding of V (and of course adding separation and replacement axioms for formulas involving j). Another way is to use a class theory such as NBG or KM. A third way is to treat Kunen's theorem as a countable infinite collection of theorems, one for each formula φ. (It is possible to have elementary embeddings of models of ZFC into themselves assuming a mild large cardinal hypothesis, but these elementary embeddings are not classes of the model.)
Kunen (1971) proved Kunen's inconsistency theorem showing that the existence of such an embedding contradicts NBG with the axiom of choice (and ZFC extended by j), but it is consistent with weaker class theories. His proof uses the axiom of choice, and it is still an open question as to whether such an embedding is consistent with NBG without the axiom of choice (or with ZF plus the extra symbol j and its attendant axioms).
Reinhardt cardinals are essentially the largest ones that have been defined (as of 2006) that are not known to be inconsistent in ZF-set theory.
References
- Jensen, Ronald (1995), "Inner Models and Large Cardinals", The Bulletin of Symbolic Logic (The Bulletin of Symbolic Logic, Vol. 1, No. 4) 1 (4): 393–407., doi:10.2307/421129, JSTOR 421129
- Kanamori, Akihiro (2003), The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings (2nd ed.), Springer, ISBN 3-540-00384-3
- Kunen, Kenneth (1971), "Elementary embeddings and infinitary combinatorics", J. Symbolic Logic (The Journal of Symbolic Logic, Vol. 36, No. 3) 36 (3): 407–413, doi:10.2307/2269948, JSTOR 2269948, MR0311478
- Reinhardt, W. N. (1967), Topics in the metamathematics of set theory, Doctoral dissertation, University of California, Berkeley
- Reinhardt, W. N. (1974), "Remarks on reflection principles, large cardinals, and elementary embeddings.", Axiomatic set theory, Proc. Sympos. Pure Math., XIII, Part II, Providence, R. I.: Amer. Math. Soc., pp. 189–205, MR0401475