Reflectivity

In optics and photometry, reflectivity is the fraction of incident radiation reflected by a surface. In general it must be treated as a directional property that is a function of the reflected direction, the incident direction, and the incident wavelength. However it is also commonly averaged over the reflected hemisphere to give the hemispherical spectral reflectivity:

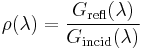
$\rho(\lambda) = \frac{G_{\mathrm{refl}}(\lambda)}{G_{\mathrm{incid}}(\lambda)}$

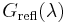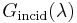where $G_{\mathrm{refl}}(\lambda)$ and $G_{\mathrm{incid}}(\lambda)$ are the reflected and incident spectral (per wavelength) intensity, respectively.

This can be further averaged over all wavelengths (in a given band of interest—say, optical) to give the total hemispherical reflectivity, or reflectance factor:

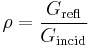
$\rho = \frac{G_{\mathrm{refl}}}{G_{\mathrm{incid}}}$

1 Reflectance
2 Surface type
3 Water reflectivity
4 Grating efficiency
5 Applications
6 See also
7 References
8 External links

Reflectance

Reflectivity and reflectance generally refer to the fraction of incident electromagnetic power that is reflected at an interface, while the term "reflection coefficient" is used for the fraction of electric field reflected.^[1]^[2] The reflectance or reflectivity is thus the square of the magnitude of the reflection coefficient.^[3] The reflection coefficient can be expressed as a complex number as determined by the Fresnel equations for a single layer, whereas the reflectance (or reflectivity) is always a positive real number.

According to the CIE (the International Commission on Illumination),^[4] reflectivity is distinguished from reflectance by the fact that reflectivity is a value that applies to thick reflecting objects.^[5] When reflection occurs from thin layers of material, internal reflection effects can cause the reflectance to vary with surface thickness. Reflectivity is the limit value of reflectance as the surface becomes thick; it is the intrinsic reflectance of the surface, hence irrespective of other parameters such as the reflectance of the rear surface. Another way to interpret this is that the reflectance is the fraction of electromagnetic power reflected from a specific sample, while reflectivity is a property of the material itself, which would be measured on a perfect machine if the material filled half of all space.^[6]

The reflectance spectrum or spectral reflectance curve is the plot of the reflectance as a function of wavelength.

Surface type

Going back to the fact that reflectivity is a directional property, most surfaces can be divided into those that give specular reflection and those that give diffuse reflection.

For specular surfaces, such as glass or polished metal, reflectivity will be nearly zero at all angles except at the appropriate reflected angle - that is, reflected radiation will follow a different path from incident radiation for all cases other than radiation normal to the surface.

For diffuse surfaces, such as matte white paint, reflectivity is uniform; radiation is reflected in all angles equally or near-equally. Such surfaces are said to be Lambertian.

Most real objects have some mixture of diffuse and specular reflective properties.

Water reflectivity

Reflection occurs when light moves from a medium with one index of refraction into a second medium with a different index of refraction.

Specular reflection from a body of water is calculated by the Fresnel equations^[7]. Fresnel reflection is directional and therefore does not contribute significantly to albedo which is primarily diffuse reflection.

A real water surface may be wavy. Reflectivity assuming a flat surface as given by the Fresnel equations can be adjusted to account for waviness.

Grating efficiency

The generalization of reflectance to a diffraction grating, which disperses light by wavelength, is called diffraction efficiency.

Applications

Reflectivity is an important concept in the fields of optics, solar thermal energy, telecommunication and radar.

References

^[7]

^ Klein and Furtak, Optics
^ Born and Wolf, Principles of Optics
^ E. Hecht (2001). Optics (4th ed.). Pearson Education. ISBN 0805385665.
^ CIE (the International Commission on Illumination)
^ CIE International Lighting Vocabulary
^ Palmer and Grant, The Art of Radiometry
^ ^a ^b Ottaviani, M. and Stamnes, K. and Koskulics, J. and Eide, H. and Long, S.R. and Su, W. and Wiscombe, W., 2008: 'Light Reflection from Water Waves: Suitable Setup for a Polarimetric Investigation under Controlled Laboratory Conditions. Journal of Atmospheric and Oceanic Technology, 25 (5), 715--728.

External links

Reflectance Data Painted surfaces etc.
Grating efficiency