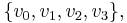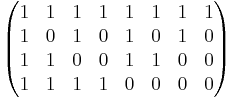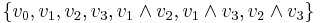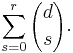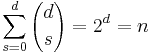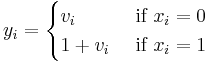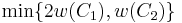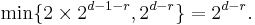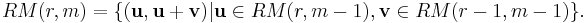Reed–Muller code
| Reed-Muller code RM(r,m) | |
|---|---|
| Named after | Irving S. Reed and David E. Muller |
| Classification | |
| Type | Linear block code |
| Parameters | |
| Block length | 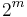 |
| Message length |  depending on depending on  and and  |
| Rate | 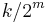 |
| Distance | 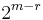 |
| Alphabet size | 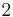 |
| Notation | ![[2^m,k,2^{m-r}]_2](/2012-wikipedia_en_all_nopic_01_2012/I/ce67c15fcc019804d04519d3b1764dcf.png) |
Reed–Muller codes are a family of linear error-correcting codes used in communications. Reed–Muller codes belong to the classes of locally testable codes and locally decodable codes, which is why they are useful in the design of probabilistically checkable proofs in computational complexity theory. They are named after their discoverers, Irving S. Reed and David E. Muller. Muller discovered the codes, and Reed proposed the majority logic decoding for the first time. Special cases of Reed–Muller codes include the Hadamard code, the Walsh–Hadamard code, and the Reed–Solomon code.
Reed–Muller codes are listed as RM(d, r), where d is the order of the code, and r determines the length of code, n = 2 r. RM codes are related to binary functions on field GF(2 r) over the elements {0, 1}.
RM(0, r) codes are repetition codes of length n = 2 r, rate 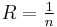 and minimum distance dmin = n.
and minimum distance dmin = n.
RM(1, r) codes are parity check codes of length n = 2 r, rate 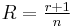 and minimum distance
and minimum distance 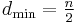 .
.
RM(r − 1, r) codes are parity check codes of length n = 2 r.
RM(r − 2, r) codes are the family of extended Hamming codes of length n = 2 r with minimum distance dmin = 4.[1]
Contents |
Construction
A generating matrix for a Reed–Muller code of length n = 2d can be constructed like this. Let us write:
Note that each member of the set X is a point in 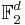 . We define in n-dimensional space
. We define in n-dimensional space 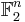 the indicator vectors
the indicator vectors
on subsets  by:
by:
together with, also in  , the binary operation
, the binary operation
referred to as the wedge product (this wedge product is not to be confused with the wedge product defined in exterior algebra). Here, 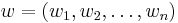 and
and 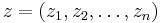 are points in
are points in 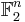 , and the operation
, and the operation  is the usual multiplication in the field
is the usual multiplication in the field 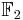 .
.
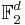 is a d-dimensional vector space over the field
is a d-dimensional vector space over the field 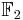 , so it is possible to write
, so it is possible to write

We define in n-dimensional space 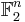 the following vectors with length n: v0 = (1, 1, 1, 1, 1, 1, 1, 1) and
the following vectors with length n: v0 = (1, 1, 1, 1, 1, 1, 1, 1) and
where the Hi are hyperplanes in 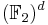 (with dimension d −1):
(with dimension d −1):
The Reed–Muller RM(d, r) code of order r and length n = 2d is the code generated by v0 and the wedge products of up to r of the vi (where by convention a wedge product of fewer than one vector is the identity for the operation).
Example 1
Let r = 3. Then n = 8, and
and
The RM(1,3) code is generated by the set
or more explicitly by the rows of the matrix
Example 2
The RM(2,3) code is generated by the set:
or more explicitly by the rows of the matrix:
Properties
The following properties hold:
1 The set of all possible wedge products of up to d of the vi form a basis for 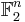 .
.
2 The RM (d, r) code has rank
3 RM (d, r) = RM (d − 1, r) | RM (d − 1, r − 1) where '|' denotes the bar product of two codes.
4 RM (d, r) has minimum Hamming weight 2d − r.
Proof
1
- There are
- such vectors and
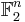 has dimension n so it is sufficient to check that the n vectors span; equivalently it is sufficient to check that RM(d, d) =
has dimension n so it is sufficient to check that the n vectors span; equivalently it is sufficient to check that RM(d, d) = 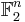 .
.
- Let x be an element of X and define
- Then
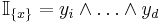
- Expansion via the distributivity of the wedge product gives
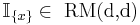 . Then since the vectors
. Then since the vectors 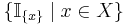 span
span 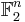 we have RM(d, d) =
we have RM(d, d) = 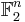 .
.
2
- By 1, all such wedge products must be linearly independent, so the rank of RM(d, r) must simply be the number of such vectors.
3
- Omitted.
4
- By induction.
- The RM(d, 0) code is the repetition code of length n =2d and weight n = 2d−0 = 2d−0. By 1 RM(d, d) =
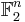 and has weight 1 = 20 = 2d−d.
and has weight 1 = 20 = 2d−d.
- The article bar product (coding theory) gives a proof that the weight of the bar product of two codes C1 , C2 is given by
- If 0 < r < d and if
- i) RM(d − 1, r) has weight 2d−1−r
- ii) RM(d-1,r-1) has weight 2d−1−(r−1) = 2d−r
- then the bar product has weight
Alternative construction
A Reed–Muller code RM(r,m) exists for any integers 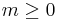 and
and 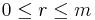 . RM(m, m) is defined as the universe (
. RM(m, m) is defined as the universe (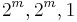 ) code. RM(−1,m) is defined as the trivial code (
) code. RM(−1,m) is defined as the trivial code (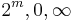 ). The remaining RM codes may be constructed from these elementary codes using the length-doubling construction
). The remaining RM codes may be constructed from these elementary codes using the length-doubling construction
From this construction, RM(r,m) is a binary linear block code (n, k, d) with length n = 2 m, dimension 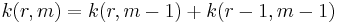 and minimum distance
and minimum distance 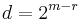 for
for 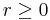 . The dual code to RM(r,m) is RM(m-r-1,m). This shows that repetition and SPC codes are duals, biorthogonal and extended Hamming codes are duals and that codes with k=n/2 are self-dual.
. The dual code to RM(r,m) is RM(m-r-1,m). This shows that repetition and SPC codes are duals, biorthogonal and extended Hamming codes are duals and that codes with k=n/2 are self-dual.
Construction based on low-degree polynomials over a finite field
There is another, simple way to construct Reed–Muller codes based on low-degree polynomials over a finite field. This construction is particularly suited for their application as locally testable codes and locally decodable codes.[2]
Let 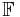 be a finite field and let
be a finite field and let  and
and  be positive integers, where
be positive integers, where  should be thought of as larger than
should be thought of as larger than  . We are going to encode messages consisting of
. We are going to encode messages consisting of 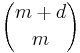 elements of
elements of 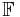 as codewords of length
as codewords of length 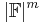 as follows: We interpret the message as an
as follows: We interpret the message as an  -variate polynomial
-variate polynomial  of degree at most
of degree at most  with coefficient from
with coefficient from 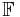 . Such a polynomial has
. Such a polynomial has 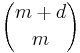 coefficients. The Reed–Muller encoding of
coefficients. The Reed–Muller encoding of  is the list of the evaluations of
is the list of the evaluations of  on all
on all 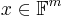 ; the codeword at the position indexed by
; the codeword at the position indexed by 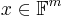 has value
has value  .
.
Table of Reed–Muller codes
The table below lists the RM(r, m) codes of lengths up to 32.
| RM(m,m) ( 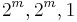 ) ) |
universe codes | ||||||
| RM(5,5) (32,32,1) |
|||||||
| RM(4,4) (16,16,1) |
RM(m − 1, m) ( 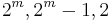 ) ) |
SPC codes | |||||
| RM(3,3) (8,8,1) |
RM(4,5) (32,31,2) |
||||||
| RM(2,2) (4,4,1) |
RM(3,4) (16,15,2) |
RM(m − 2, m) ( 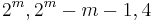 ) ) |
ext. Hamming codes | ||||
| RM(1,1) (2,2,1) |
RM(2,3) (8,7,2) |
RM(3,5) (32,26,4) |
|||||
| RM(0,0) (1,1,1) |
RM(1,2) (4,3,2) |
RM(2,4) (16,11,4) |
|||||
| RM(0,1) (2,1,2) |
RM(1,3) (8,4,4) |
RM(2,5) (32,16,8) |
self-dual codes | ||||
| RM(−1,0) (1,0, 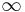 ) ) |
RM(0,2) (4,1,4) |
RM(1,4) (16,5,8) |
|||||
| RM(-1,1) (2,0, 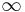 ) ) |
RM(0,3) (8,1,8) |
RM(1,5) (32,6,16) |
|||||
| RM(-1,2) (4,0, 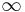 ) ) |
RM(0,4) (16,1,16) |
RM(1,m) ( 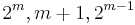 ) ) |
biorthogonal codes | ||||
| RM(−1,3) (8,0, 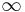 ) ) |
RM(0,5) (32,1,32) |
||||||
| RM(−1,4) (16,0, 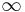 ) ) |
RM(0,m) ( 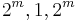 ) ) |
repetition codes | |||||
| RM(−1,5) (32,0, 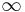 ) ) |
|||||||
| RM(-1,m) ( 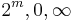 ) ) |
trivial codes |
Decoding RM codes
RM(r, m) codes can be decoded using the majority logic decoding. The basic idea of majority logic decoding is to build several checksums for each received code word element. Since each of the different checksums must all have the same value (i.e the value of the message word element weight), we can use a majority logic decoding to decipher the value of the message word element. Once each order of the polynomial is decoded, the received word is modified accordingly by removing the corresponding codewords weighted by the decoded message contributions, up to the present stage. So for a rth order RM code, we have to decode iteratively r+1, times before we arrive at the final received code-word. Also, the values of the message bits are calculated through this scheme; finally we can calculate the codeword by multiplying the message word (just decoded) with the generator matrix.
One clue if the decoding succeeded, is to have an all-zero modified received word, at the end of (r + 1)-stage decoding through the majority logic decoding. This technique was proposed by Irving S. Reed, and is more general when applied to other finite geometry codes.
Notes
- ^ Trellis and Turbo Coding, C. Schlegel & L. Perez, Wiley Interscience, 2004, p149.
- ^ Prahladh Harsha et al., Limits of Approximation Algorithms: PCPs and Unique Games (DIMACS Tutorial Lecture Notes), Section 5.2.1.
References
Research Articles:
- D. E. Muller. Application of boolean algebra to switching circuit design and to error detection. IRE Transactions on Electronic Computers, 3:6–12, 1954.
- Irving S. Reed. A class of multiple-error-correcting codes and the decoding scheme. Transactions of the IRE Professional Group on Information Theory, 4:38–49, 1954.
Textbooks:
- Shu Lin; Daniel Costello (2005). Error Control Coding (2nd ed ed.). Pearson. ISBN 0130179736. Chapter 4.
- J.H. van Lint (1992). Introduction to Coding Theory. GTM. 86 (2nd ed ed.). Springer-Verlag. ISBN 3-540-54894-7. Chapter 4.5.
External links
- MIT OpenCourseWare, 6.451 Principles of Digital Communication II, Lecture Notes section 6.4
- GPL Matlab-implementation of RM-codes
|
||||||||||||||||||||||||||
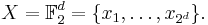
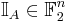
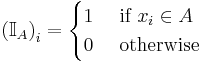
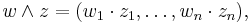
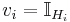
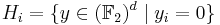
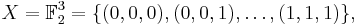
![\begin{matrix}
v_0 & = & (1,1,1,1,1,1,1,1) \\[2pt]
v_1 & = & (1,0,1,0,1,0,1,0) \\[2pt]
v_2 & = & (1,1,0,0,1,1,0,0) \\[2pt]
v_3 & = & (1,1,1,1,0,0,0,0). \\
\end{matrix}](/2012-wikipedia_en_all_nopic_01_2012/I/43333a43b3ef7770e7b995f2bce95696.png)