Reeb stability theorem
In mathematics, Reeb stability theorem, named after Georges Reeb, asserts that if one leaf of a codimension-one foliation is closed and has finite fundamental group, then all the leaves are closed and have finite fundamental group.
Contents |
Reeb local stability theorem
Theorem[1]: Let  be a
be a 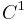 , codimension
, codimension  foliation of a manifold
foliation of a manifold  and
and  a compact leaf with finite holonomy group. There exists a neighborhood
a compact leaf with finite holonomy group. There exists a neighborhood  of
of  , saturated in
, saturated in  (also called invariant), in which all the leaves are compact with finite holonomy groups. Further, we can define a retraction
(also called invariant), in which all the leaves are compact with finite holonomy groups. Further, we can define a retraction 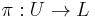 such that, for every leaf
such that, for every leaf 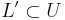 ,
, 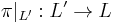 is a covering with a finite number of sheets and, for each
is a covering with a finite number of sheets and, for each 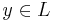 ,
, 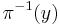 is homeomorphic to a disk of dimension k and is transverse to
is homeomorphic to a disk of dimension k and is transverse to  . The neighborhood
. The neighborhood  can be taken to be arbitrarily small.
can be taken to be arbitrarily small.
The last statement means in particular that, in a neighborhood of the point corresponding to a compact leaf with finite holonomy, the space of leaves is Hausdorff. Under certain conditions the Reeb Local Stability Theorem may replace the Poincaré–Bendixson theorem in higher dimensions.[2] This is the case of codimension one, singular foliations 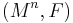 , with
, with 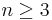 , and some center-type singularity in
, and some center-type singularity in 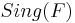 .
.
The Reeb Local Stability Theorem also has a version for a noncompact leaf.[3][4]
Reeb global stability theorem
An important problem in foliation theory is the study of the influence exerted by a compact leaf upon the global structure of a foliation. For certain classes of foliations, this influence is considerable.
Theorem[1]: Let  be a
be a 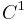 , codimension one foliation of a closed manifold
, codimension one foliation of a closed manifold  . If
. If  contains a compact leaf
contains a compact leaf  with finite fundamental group, then all the leaves of
with finite fundamental group, then all the leaves of  are compact, with finite fundamental group. If
are compact, with finite fundamental group. If  is transversely orientable, then every leaf of
is transversely orientable, then every leaf of  is diffeomorphic to
is diffeomorphic to  ;
;  is the total space of a fibration
is the total space of a fibration 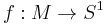 over
over 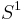 , with fibre
, with fibre  , and
, and  is the fibre foliation,
is the fibre foliation, 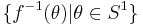 .
.
This theorem holds true even when  is a foliation of a manifold with boundary, which is, a priori, tangent on certain components of the boundary and transverse on other components.[5] In this case it implies Reeb sphere theorem.
is a foliation of a manifold with boundary, which is, a priori, tangent on certain components of the boundary and transverse on other components.[5] In this case it implies Reeb sphere theorem.
Reeb Global Stability Theorem is false for foliations of codimension greater than one.[6] However, for some special kinds of foliations one has the following global stability results:
- In the presence of a certain transverse geometric structure:
Theorem[7]: Let  be a complete conformal foliation of codimension
be a complete conformal foliation of codimension 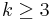 of a connected manifold
of a connected manifold  . If
. If  has a compact leaf with finite holonomy group, then all the leaves of
has a compact leaf with finite holonomy group, then all the leaves of  are compact with finite holonomy group.
are compact with finite holonomy group.
- For holomorphic foliations in complex Kähler manifold:
Theorem[8]: Let  be a holomorphic foliation of codimension
be a holomorphic foliation of codimension  in a compact complex Kähler manifold. If
in a compact complex Kähler manifold. If  has a compact leaf with finite holonomy group then every leaf of
has a compact leaf with finite holonomy group then every leaf of  is compact with finite holonomy group.
is compact with finite holonomy group.
References
- C. Camacho, A. Lins Neto: Geometric theory of foliations, Boston, Birkhauser, 1985
- I. Tamura, Topology of foliations: an introduction, Transl. of Math. Monographs, AMS, v.97, 2006, 193 p.
Notes
- ^ a b G. Reeb, G. Reeb (1952). Sur certaines propriétés toplogiques des variétés feuillétées. Actualités Sci. Indust.. 1183. Paris: Hermann.
- ^ J. Palis, jr., W. de Melo, Geometric theory of dinamical systems: an introduction, — New-York, Springer,1982.
- ^ T.Inaba,
 Reeb stability of noncompact leaves of foliations,— Proc. Japan Acad. Ser. A Math. Sci., 59:158{160, 1983 [1]
Reeb stability of noncompact leaves of foliations,— Proc. Japan Acad. Ser. A Math. Sci., 59:158{160, 1983 [1] - ^ J. Cantwell and L. Conlon, Reeb stability for noncompact leaves in foliated 3-manifolds, — Proc. Amer.Math.Soc. 33 (1981), no. 2, 408–410.[2]
- ^ C. Godbillon, Feuilletages, etudies geometriques, — Basel, Birkhauser, 1991
- ^ W.T.Wu and G.Reeb, Sur les éspaces fibres et les variétés feuillitées, — Hermann, 1952.
- ^ R.A. Blumenthal, Stability theorems for conformal foliations, — Proc. AMS. 91, 1984, p. 55–63. [3]
- ^ J.V. Pereira, Global stability for holomorphic foliations on Kaehler manifolds, — Qual. Theory Dyn. Syst. 2 (2001), 381–384. arXiv:math/0002086v2