Reconstruction conjecture

Unsolved problems in mathematics
Are graphs uniquely determined by their subgraphs?

Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly^[1] and Ulam.^[2]

1 Formal statements
2 Verification
- 2.1 Reconstructible graph families
3 Recognizable properties
4 Reduction
5 Other structures
6 See also
7 Further reading
8 References

Formal statements

Given a graph 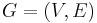$G = (V,E)$ , a vertex-deleted subgraph of $G$ is a subgraph formed by deleting exactly one vertex from $G$ . Clearly, it is an induced subgraph of $G$ .

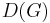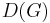For a graph $G$ , the deck of G, denoted $D(G)$ , is the multiset of all vertex-deleted subgraphs of $G$ . Each graph in $D(G)$ is called a card. Two graphs that have the same deck are said to be hypomorphic.

With these definitions, the conjecture can be stated as:

Reconstruction Conjecture: Any two hypomorphic graphs on at least three vertices are isomorphic.

(The requirement that the graphs have at least three vertices is necessary because both graphs on two vertices have the same decks.)

Harary^[3] suggested a stronger version of the conjecture:

Set Reconstruction Conjecture: Any two graphs on at least four vertices with the same sets of vertex-deleted subgraphs are isomorphic.

Given a graph 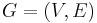$G = (V,E)$ , an edge-deleted subgraph of $G$ is a subgraph formed by deleting exactly one edge from $G$ .

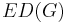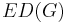For a graph $G$ , the edge-deck of G, denoted $ED(G)$ , is the multiset of all edge-deleted subgraphs of $G$ . Each graph in $ED(G)$ is called an edge-card.

Edge Reconstruction Conjecture: (Harary, 1964)^[3] Any two graphs with at least four edges and having the same edge-decks are isomorphic.

Verification

Both the reconstruction and set reconstruction conjectures have been verified for all graphs with at most 11 vertices (McKay^[4]).

In a probabilistic sense, it has been shown (Bollobás^[5]) that almost all graphs are reconstructible. This means that the probability that a randomly chosen graph on $n$ vertices is not reconstructible goes to 0 as $n$ goes to infinity. In fact, it was shown that not only are almost all graphs reconstructible, but in fact that the entire deck is not necessary to reconstruct them — almost all graphs have the property that there exist three cards in their deck that uniquely determine the graph.

Reconstructible graph families

The conjecture has been verified for a number of infinite classes of graphs.

Regular graphs^[6]
Trees^[6]
Disconnected graphs^[6]
Unit interval graphs ^[7]
Separable graphs without end vertices
Maximal Planar Graphs
Maximal Outerplanar Graphs
Outer Planar Graphs
Critical blocks

Recognizable properties

In context of the reconstruction conjecture, a graph property is called recognizable if one can determine the property from the deck of a graph. The following properties of graphs are recognizable:

Degree sequence
Tutte polynomial
Planarity
The types of spanning trees in a graph
Chromatic polynomial
Being a perfect graph or an interval graph, or some other subclasses of perfect graphs ^[7]

Reduction

The reconstruction conjecture is true if all 2-connected graphs are reconstructible ^[8]

Other structures

It has been shown that the following are not in general reconstructible:

Digraphs: Infinite families of non-reconstructible digraphs are known, including tournaments (Stockmeyer^[9]) and non-tournaments (Stockmeyer^[10]). A tournament is reconstructible if it is not strongly connected.^[11]
Hypergraphs (Kocay^[12]).
Infinite graphs. Let T be a tree on an infinite number of vertices such that every vertex has infinite degree. The counterexample is T and 2T. The question of reconstructibility for locally finite infinite graphs is still open.

References

^ Kelly, P. J., A congruence theorem for trees, Pacific J. Math., 7 (1957), 961–968.
^ Ulam, S. M., A collection of mathematical problems, Wiley, New York, 1960.
^ ^a ^b Harary, F., On the reconstruction of a graph from a collection of subgraphs. In Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963). Publ. House Czechoslovak Acad. Sci., Prague, 1964, pp. 47–52.
^ McKay, B. D., Small graphs are reconstructible, Australas. J. Combin., 15 (1997), 123–126.
^ Bollobás, B., Almost every graph has reconstruction number three, J. Graph Theory, 14 (1990), 1–4.
^ ^a ^b ^c Harary, F. (1974), "A survey of the reconstruction conjecture", A survey of the reconstruction conjecture, Graphs and Combinatorics. Lecture Notes in Mathematics 406, 406, Springer, pp. 18–28, doi:10.1007/BFb0066431
^ ^a ^b von Rimscha, M.: Reconstructibility and perfect graphs. Discrete Mathematics 47, 283–291 (1983)
^ Yang Yongzhi:The reconstruction conjecture is true if all 2-connected graphs are reconstructible. Journal of graph theory 12, 237–243 (1988)
^ Stockmeyer, P. K., The falsity of the reconstruction conjecture for tournaments, J. Graph Theory, 1 (1977), 19–25.
^ Stockmeyer, P. K., A census of non-reconstructable digraphs, I: six related families, J. Combin. Theory Ser. B, 31 (1981), 232–239.
^ Harary, F. and Palmer, E., On the problem of reconstructing a tournament from sub-tournaments, Monatsh. Math., 71 (1967), 14–23.
^ Kocay, W. L., A family of nonreconstructible hypergraphs, J. Combin. Theory Ser. B, 42 (1987), 46–63.
^ Nash-Williams, C. St. J. A., The Reconstruction Problem, in Selected topics in graph theory, 205–236 (1978).