Realizability
Realizability is a part of proof theory which can be used to handle information about formulas instead of about the proofs of formulas.[1] A natural number n is said to realize a statement in the language of arithmetic of natural numbers. Other logical and mathematical statements are also realizable, providing a method for interpreting well formed formulas without resorting to proofs for arriving at those formulas.
Contents |
Origins
Kleene introduced the concept of realizability in 1945 in the hopes of it being a faithful mirror of intuitionistic reasoning,[2] but this conjecture was first disproved by Rose with his example of realizable propositional formulas that are unprovable in intuitionist calculus.[3] Realizability appears to defy axiomatization due to its complexity, but it may be approachable through a higher-order Heyting arithmetic (HA). For HA3, a completeness property for the category of modest sets may be proved from the axioms which characterize the realizability of HA3.[4]
Later developments
The modified realizability[5] uses typed lambda calculus as the language of realizers. Modified realizability is one way to show that Markov's principle is not derivable in intuitionistic logic. On the contrary, it allows to constructively justify the principle of independence of premisses: 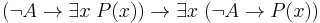 .
.
Relative realizability[6] is an intuitionist analysis of recursive or recursively enumerable elements of data structures that are not necessarily computable, such as computable operations on all real numbers when reals can be only approximated on digital computer systems.
Applications in computer science
Modified realizability justifies the process of program extraction implemented in some proof assistants such as Coq.
References
- Birkedal, Lars; Jaap van Oosten (2000). Relative and modified relative realizability. http://www.itu.dk/people/birkedal/papers/relmrr.ps.gz.
- Kreisel G. (1959). "Interpretation of Analysis by Means of Constructive Functionals of Finite Types", in: Constructivity in Mathematics, edited by A. Heyting, North-Holland, pp. 101–128.
- Kleene, S. C. (1945). "On the interpretation of intuitionistic number theory". Journal of Symbolic Logic 10 (4): 109–124. doi:10.2307/2269016. JSTOR 2269016.
- Kleene, S. C. (1973). "Realizability: a retrospective survey" from Mathias, A. R. D.; Hartley Rogers (1973). Cambridge Summer School in Mathematical Logic : held in Cambridge/England, August 1–21, 1971. Berlin: Springer. ISBN 3-540-05569-X., pp. 95–112.
- Oosten, Jaap van (2000). Realizability: An Historical Essay. http://www.math.uu.nl/people/jvoosten/realizability/history.ps.gz.
- Rose, G. F. (1953). "Propositional calculus and realizability". Transactions of the American Mathematical Society 75 (1): 1–19. doi:10.2307/1990776. JSTOR 1990776.
External links
- Realizability Collection of links to recent papers on realizability and related topics.