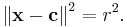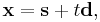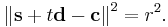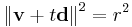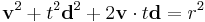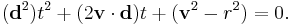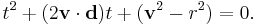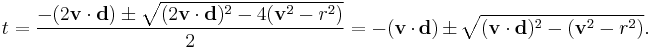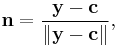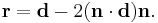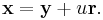Ray tracing (graphics)

Not to be confused with Ray casting.

In computer graphics, ray tracing is a technique for generating an image by tracing the path of light through pixels in an image plane and simulating the effects of its encounters with virtual objects. The technique is capable of producing a very high degree of visual realism, usually higher than that of typical scanline rendering methods, but at a greater computational cost. This makes ray tracing best suited for applications where the image can be rendered slowly ahead of time, such as in still images and film and television special effects, and more poorly suited for real-time applications like video games where speed is critical. Ray tracing is capable of simulating a wide variety of optical effects, such as reflection and refraction, scattering, and dispersion phenomena (such as chromatic aberration).

1 Algorithm overview
2 Detailed description of ray tracing computer algorithm and its genesis
3 In real time
4 Example
5 See also
6 References
7 External links

Algorithm overview

Optical ray tracing describes a method for producing visual images constructed in 3D computer graphics environments, with more photorealism than either ray casting or scanline rendering techniques. It works by tracing a path from an imaginary eye through each pixel in a virtual screen, and calculating the color of the object visible through it.

Scenes in raytracing are described mathematically by a programmer or by a visual artist (typically using intermediary tools). Scenes may also incorporate data from images and models captured by means such as digital photography.

Typically, each ray must be tested for intersection with some subset of all the objects in the scene. Once the nearest object has been identified, the algorithm will estimate the incoming light at the point of intersection, examine the material properties of the object, and combine this information to calculate the final color of the pixel. Certain illumination algorithms and reflective or translucent materials may require more rays to be re-cast into the scene.

It may at first seem counterintuitive or "backwards" to send rays away from the camera, rather than into it (as actual light does in reality), but doing so is many orders of magnitude more efficient. Since the overwhelming majority of light rays from a given light source do not make it directly into the viewer's eye, a "forward" simulation could potentially waste a tremendous amount of computation on light paths that are never recorded. A computer simulation that starts by casting rays from the light source is called Photon mapping, and it takes much longer than a comparable ray trace.

Therefore, the shortcut taken in raytracing is to presuppose that a given ray intersects the view frame. After either a maximum number of reflections or a ray traveling a certain distance without intersection, the ray ceases to travel and the pixel's value is updated. The light intensity of this pixel is computed using a number of algorithms, which may include the classic rendering algorithm and may also incorporate techniques such as radiosity.

Detailed description of ray tracing computer algorithm and its genesis

What happens in nature

In nature, a light source emits a ray of light which travels, eventually, to a surface that interrupts its progress. One can think of this "ray" as a stream of photons traveling along the same path. In a perfect vacuum this ray will be a straight line (ignoring relativistic effects). In reality, any combination of four things might happen with this light ray: absorption, reflection, refraction and fluorescence. A surface may absorb part of the light ray, resulting in a loss of intensity of the reflected and/or refracted light. It might also reflect all or part of the light ray, in one or more directions. If the surface has any transparent or translucent properties, it refracts a portion of the light beam into itself in a different direction while absorbing some (or all) of the spectrum (and possibly altering the color). Less commonly, a surface may absorb some portion of the light and fluorescently re-emit the light at a longer wavelength colour in a random direction, though this is rare enough that it can be discounted from most rendering applications. Between absorption, reflection, refraction and fluorescence, all of the incoming light must be accounted for, and no more. A surface cannot, for instance, reflect 66% of an incoming light ray, and refract 50%, since the two would add up to be 116%. From here, the reflected and/or refracted rays may strike other surfaces, where their absorptive, refractive, reflective and fluorescent properties again affect the progress of the incoming rays. Some of these rays travel in such a way that they hit our eye, causing us to see the scene and so contribute to the final rendered image.

Ray casting algorithm

Main article: Ray casting

The first ray casting (versus ray tracing) algorithm used for rendering was presented by Arthur Appel^[1] in 1968. The idea behind ray casting is to shoot rays from the eye, one per pixel, and find the closest object blocking the path of that ray – think of an image as a screen-door, with each square in the screen being a pixel. This is then the object the eye normally sees through that pixel. Using the material properties and the effect of the lights in the scene, this algorithm can determine the shading of this object. The simplifying assumption is made that if a surface faces a light, the light will reach that surface and not be blocked or in shadow. The shading of the surface is computed using traditional 3D computer graphics shading models. One important advantage ray casting offered over older scanline algorithms is its ability to easily deal with non-planar surfaces and solids, such as cones and spheres. If a mathematical surface can be intersected by a ray, it can be rendered using ray casting. Elaborate objects can be created by using solid modeling techniques and easily rendered.

Ray tracing algorithm

The next important research breakthrough came from Turner Whitted in 1979.^[2] Previous algorithms cast rays from the eye into the scene until they hit an object, but the rays were traced no further. Whitted continued the process. When a ray hits a surface, it could generate up to three new types of rays: reflection, refraction, and shadow.^[3] A reflected ray continues on in the mirror-reflection direction from a shiny surface. It is then intersected with objects in the scene; the closest object it intersects is what will be seen in the reflection. Refraction rays traveling through transparent material work similarly, with the addition that a refractive ray could be entering or exiting a material. To further avoid tracing all rays in a scene, a shadow ray is used to test if a surface is visible to a light. A ray hits a surface at some point. If the surface at this point faces a light, a ray (to the computer, a line segment) is traced between this intersection point and the light. If any opaque object is found in between the surface and the light, the surface is in shadow and so the light does not contribute to its shade. This new layer of ray calculation added more realism to ray traced images.

Advantages over other rendering methods

Ray tracing's popularity stems from its basis in a realistic simulation of lighting over other rendering methods (such as scanline rendering or ray casting). Effects such as reflections and shadows, which are difficult to simulate using other algorithms, are a natural result of the ray tracing algorithm. Relatively simple to implement yet yielding impressive visual results, ray tracing often represents a first foray into graphics programming. The computational independence of each ray makes ray tracing amenable to parallelization.^[4]

Disadvantages

A serious disadvantage of ray tracing is performance. Scanline algorithms and other algorithms use data coherence to share computations between pixels, while ray tracing normally starts the process anew, treating each eye ray separately. However, this separation offers other advantages, such as the ability to shoot more rays as needed to perform anti-aliasing and improve image quality where needed. Although it does handle interreflection and optical effects such as refraction accurately, traditional ray tracing is also not necessarily photorealistic. True photorealism occurs when the rendering equation is closely approximated or fully implemented. Implementing the rendering equation gives true photorealism, as the equation describes every physical effect of light flow. However, this is usually infeasible given the computing resources required. The realism of all rendering methods, then, must be evaluated as an approximation to the equation, and in the case of ray tracing, it is not necessarily the most realistic. Other methods, including photon mapping, are based upon ray tracing for certain parts of the algorithm, yet give far better results.

Reversed direction of traversal of scene by the rays

The process of shooting rays from the eye to the light source to render an image is sometimes called backwards ray tracing, since it is the opposite direction photons actually travel. However, there is confusion with this terminology. Early ray tracing was always done from the eye, and early researchers such as James Arvo used the term backwards ray tracing to mean shooting rays from the lights and gathering the results. Therefore it is clearer to distinguish eye-based versus light-based ray tracing.

While the direct illumination is generally best sampled using eye-based ray tracing, certain indirect effects can benefit from rays generated from the lights. Caustics are bright patterns caused by the focusing of light off a wide reflective region onto a narrow area of (near-)diffuse surface. An algorithm that casts rays directly from lights onto reflective objects, tracing their paths to the eye, will better sample this phenomenon. This integration of eye-based and light-based rays is often expressed as bidirectional path tracing, in which paths are traced from both the eye and lights, and the paths subsequently joined by a connecting ray after some length.^[5]^[6]

Photon mapping is another method that uses both light-based and eye-based ray tracing; in an initial pass, energetic photons are traced along rays from the light source so as to compute an estimate of radiant flux as a function of 3-dimensional space (the eponymous photon map itself). In a subsequent pass, rays are traced from the eye into the scene to determine the visible surfaces, and the photon map is used to estimate the illumination at the visible surface points.^[7]^[8] The advantage of photon mapping versus bidirectional path tracing is the ability to achieve significant reuse of photons, reducing computation, at the cost of statistical bias.

An additional problem occurs when light must pass through a very narrow aperture to illuminate the scene (consider a darkened room, with a door slightly ajar leading to a brightly-lit room), or a scene in which most points do not have direct line-of-sight to any light source (such as with ceiling-directed light fixtures or torchieres). In such cases, only a very small subset of paths will transport energy; Metropolis light transport is a method which begins with a random search of the path space, and when energetic paths are found, reuses this information by exploring the nearby space of rays.^[9]

To the right is an image showing a simple example of a path of rays recursively generated from the camera (or eye) to the light source using the above algorithm. A diffuse surface reflects light in all directions.

First, a ray is created at an eyepoint and traced through a pixel and into the scene, where it hits a diffuse surface. From that surface the algorithm recursively generates a reflection ray, which is traced through the scene, where it hits another diffuse surface. Finally, another reflection ray is generated and traced through the scene, where it hits the light source and is absorbed. The color of the pixel now depends on the colors of the first and second diffuse surface and the color of the light emitted from the light source. For example if the light source emitted white light and the two diffuse surfaces were blue, then the resulting color of the pixel is blue.

In real time

The first implementation of a "real-time" ray-tracer was credited at the 2005 SIGGRAPH computer graphics conference as the REMRT/RT tools developed in 1986 by Mike Muuss for the BRL-CAD solid modeling system. Initially published in 1987 at USENIX, the BRL-CAD ray-tracer is the first known implementation of a parallel network distributed ray-tracing system that achieved several frames per second in rendering performance.^[10] This performance was attained by means of the highly-optimized yet platform independent LIBRT ray-tracing engine in BRL-CAD and by using solid implicit CSG geometry on several shared memory parallel machines over a commodity network. BRL-CAD's ray-tracer, including REMRT/RT tools, continue to be available and developed today as Open source software.^[11]

Since then, there have been considerable efforts and research towards implementing ray tracing in real time speeds for a variety of purposes on stand-alone desktop configurations. These purposes include interactive 3D graphics applications such as demoscene productions, computer and video games, and image rendering. Some real-time software 3D engines based on ray tracing have been developed by hobbyist demo programmers since the late 1990s.^[12]

The OpenRT project includes a highly-optimized software core for ray tracing along with an OpenGL-like API in order to offer an alternative to the current rasterisation based approach for interactive 3D graphics. Ray tracing hardware, such as the experimental Ray Processing Unit developed at the Saarland University, has been designed to accelerate some of the computationally intensive operations of ray tracing. On March 16, 2007, the University of Saarland revealed an implementation of a high-performance ray tracing engine that allowed computer games to be rendered via ray tracing without intensive resource usage.^[13]

On June 12, 2008 Intel demonstrated a special version of Enemy Territory: Quake Wars, titled Quake Wars: Ray Traced, using ray tracing for rendering, running in basic HD (720p) resolution. ETQW operated at 14-29 frames per second. The demonstration ran on a 16-core (4 socket, 4 core) Xeon Tigerton system running at 2.93 GHz.^[14]

At SIGGRAPH 2009, Nvidia announced OptiX, an API for real-time ray tracing on Nvidia GPUs. The API exposes seven programmable entry points within the ray tracing pipeline, allowing for custom cameras, ray-primitive intersections, shaders, shadowing, etc.^[15]

Example

As a demonstration of the principles involved in raytracing, let us consider how one would find the intersection between a ray and a sphere. In vector notation, the equation of a sphere with center 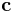$\mathbf c$ and radius 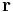$\mathbf r$ is

$\left\Vert \mathbf x - \mathbf c \right\Vert^2=r^2.$

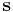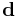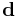Any point on a ray starting from point $\mathbf s$ with direction $\mathbf d$ (here $\mathbf d$ is a unit vector) can be written as

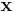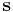$\mathbf x=\mathbf s%2Bt\mathbf d,$

where $t$ is its distance between $\mathbf x$ and $\mathbf s$ . In our problem, we know 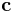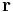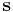$\mathbf c$ , $\mathbf r$ , $\mathbf s$ (e.g. the position of a light source) and 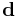$\mathbf d$ , and we need to find $t$ . Therefore, we substitute for 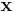$\mathbf x$ :

$\left\Vert\mathbf{s}%2Bt\mathbf{d}-\mathbf{c}\right\Vert^{2}=r^2.$

Let 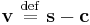$\mathbf{v}\ \stackrel{\mathrm{def}}{=}\ \mathbf{s}-\mathbf{c}$ for simplicity; then

$\left\Vert\mathbf{v}%2Bt\mathbf{d}\right\Vert^{2}=r^{2}$

$\mathbf{v}^2%2Bt^2\mathbf{d}^2%2B2\mathbf{v}\cdot t\mathbf{d}=r^2$

$(\mathbf{d}^2)t^2%2B(2\mathbf{v}\cdot\mathbf{d})t%2B(\mathbf{v}^2-r^2)=0.$

Knowing that d is a unit vector allows us this minor simplification:

$t^2%2B(2\mathbf{v}\cdot\mathbf{d})t%2B(\mathbf{v}^2-r^2)=0.$

This quadratic equation has solutions

$t=\frac{-(2\mathbf{v}\cdot\mathbf{d})\pm\sqrt{(2\mathbf{v}\cdot\mathbf{d})^2-4(\mathbf{v}^2-r^2)}}{2}=-(\mathbf{v}\cdot\mathbf{d})\pm\sqrt{(\mathbf{v}\cdot\mathbf{d})^2-(\mathbf{v}^2-r^2)}.$

The two values of $t$ found by solving this equation are the two ones such that 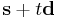$\mathbf \mathbf s%2Bt\mathbf d$ are the points where the ray intersects the sphere.

Any value which is negative does not lie on the ray, but rather in the opposite half-line (i.e. the one starting from 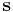$\mathbf s$ with opposite direction).

If the quantity under the square root ( the discriminant ) is negative, then the ray does not intersect the sphere.

Let us suppose now that there is at least a positive solution, and let $t$ be the minimal one. In addition, let us suppose that the sphere is the nearest object on our scene intersecting our ray, and that it is made of a reflective material. We need to find in which direction the light ray is reflected. The laws of reflection state that the angle of reflection is equal and opposite to the angle of incidence between the incident ray and the normal to the sphere.

The normal to the sphere is simply

$\mathbf n=\frac{\mathbf y- \mathbf c}{\left\Vert\mathbf y- \mathbf c\right\Vert},$

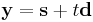where $\mathbf y=\mathbf s%2Bt\mathbf d$ is the intersection point found before. The reflection direction can be found by a reflection of 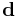$\mathbf d$ with respect to 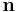$\mathbf n$ , that is

$\mathbf r = \mathbf d - 2(\mathbf n \cdot \mathbf d ) \mathbf n.$

Thus the reflected ray has equation

$\mathbf x = \mathbf y %2B u \mathbf r. \,$

Now we only need to compute the intersection of the latter ray with our field of view, to get the pixel which our reflected light ray will hit. Lastly, this pixel is set to an appropriate color, taking into account how the color of the original light source and the one of the sphere are combined by the reflection.

This is merely the math behind the line–sphere intersection and the subsequent determination of the colour of the pixel being calculated. There is, of course, far more to the general process of raytracing, but this demonstrates an example of the algorithms used.

References

^ Appel A. (1968) Some techniques for shading machine rendering of solids. AFIPS Conference Proc. 32 pp.37-45
^ Whitted T. (1979) An improved illumination model for shaded display. Proceedings of the 6th annual conference on Computer graphics and interactive techniques
^ Tomas Nikodym (June 2010). "Ray Tracing Algorithm For Interactive Applications". Czech Technical University, FEE. https://dip.felk.cvut.cz/browse/pdfcache/nikodtom_2010bach.pdf.
^ A. Chalmers, T. Davis, and E. Reinhard. Practical parallel rendering, ISBN 1568811799. AK Peters, Ltd., 2002.
^ Eric P. Lafortune and Yves D. Willems (December 1993). "Bi-Directional Path Tracing". Proceedings of Compugraphics '93: 145–153. http://www.graphics.cornell.edu/~eric/Portugal.html.
^ Péter Dornbach. "Implementation of bidirectional ray tracing algorithm". http://www.cescg.org/CESCG98/PDornbach/index.html. Retrieved 2008-06-11.
^ Global Illumination using Photon Maps
^ Photon Mapping - Zack Waters
^ http://graphics.stanford.edu/papers/metro/metro.pdf
^ See Proceedings of 4th Computer Graphics Workshop, Cambridge, MA, USA, October 1987. Usenix Association, 1987. pp 86–98.
^ "About BRL-CAD". http://brlcad.org/d/about. Retrieved 2009-07-28.
^ Piero Foscari. "The Realtime Raytracing Realm". ACM Transactions on Graphics. http://www.acm.org/tog/resources/RTNews/demos/overview.htm. Retrieved 2007-09-17.
^ Mark Ward (March 16, 2007). "Rays light up life-like graphics". BBC News. http://news.bbc.co.uk/1/hi/technology/6457951.stm. Retrieved 2007-09-17.
^ Theo Valich (June 12, 2008). "Intel converts ET: Quake Wars to ray tracing". TG Daily. http://www.tgdaily.com/html_tmp/content-view-37925-113.html. Retrieved 2008-06-16.
^ Nvidia (October 18, 2009). "Nvidia OptiX". Nvidia. http://www.nvidia.com/object/optix.html. Retrieved 2009-11-06.