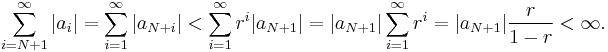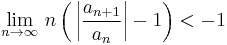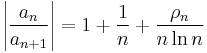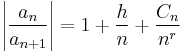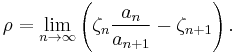Ratio test

In mathematics, the ratio test is a test (or "criterion") for the convergence of a series 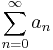$\sum_{n=0}^\infty a_n$ , where each term is a real or complex number and 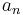$a_n$ is nonzero when n is large. The test was first published by Jean le Rond d'Alembert and is sometimes known as d'Alembert's ratio test.

1 The test
2 Examples
3 Proof
4 Extensions for L=1
- 4.1 Raabe's test
- 4.2 Higher order tests
5 See also
6 Footnotes
7 References

The test

The usual form of the test makes use of the limit

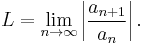
$L = \lim_{n\rightarrow\infty}\left|\frac{a_{n%2B1}}{a_n}\right|.$

(1)

The ratio test states that:

if L < 1 then the series converges absolutely;
if L > 1 then the series does not converge;
if L = 1 or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.

It is possible to make the ratio test applicable to certain cases where the limit L fails to exist, if limit superior and limit inferior are used. The test criteria can also be refined so that the test is sometimes conclusive even when L = 1. More specifically, let

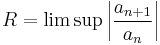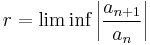$R = \lim\sup \left|\frac{a_{n%2B1}}{a_n}\right|$ and $r = \lim\inf \left|\frac{a_{n%2B1}}{a_n}\right|$ .

Then the ratio test states that:^[1]^[2]

if R < 1, the series converges absolutely;
if r > 1, the series diverges;
if 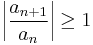$\left|\frac{a_{n%2B1}}{a_n}\right|\ge 1$ for all large n (regardless of the value of r ), the series also diverges; this is because 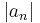$|a_n|$ is nonzero and increasing and hence 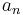$a_n$ does not approach zero;
the test is otherwise inconclusive.

If the limit L in (1) exists, we must have L=R=r. So the original ratio test is a weaker version of the refined one.

Examples

Convergent because L<1

Consider the series

$\sum_{n=1}^\infty\frac{n}{e^n}$

Putting this into the ratio test:

$L = \lim_{n\to\infty} \left| \frac{a_{n%2B1}}{a_n} \right| = \lim_{n\to\infty} \left| \frac{\frac{n%2B1}{e^{n%2B1}}}{\frac{n}{e^n}}\right| = \frac{1}{e} < 1.$

Thus the series converges.

Divergent because L>1

Consider the series

$\sum_{n=1}^\infty\frac{e^n}{n}.$

Putting this into the ratio test:

$L = \lim_{n\to\infty} \left| \frac{a_{n%2B1}}{a_n} \right| = \lim_{n\to\infty} \left| \frac{\frac{e^{n%2B1}}{n%2B1}}{\frac{e^n}{n}} \right| = e > 1.$

Thus the series diverges.

Inconclusive because L=1

Consider the three series

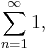
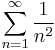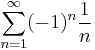$\sum_{n=1}^\infty 1,$ $\sum_{n=1}^\infty \frac{1}{n^2}$ and $\sum_{n=1}^\infty (-1)^n\frac{1}{n}$ .

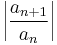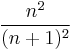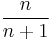The first series diverges, the second one converges absolutely and the third one converges conditionally. However, the term-by-term magnitude ratios $\left|\frac{a_{n%2B1}}{a_n}\right|$ of the three series are respectively 1, $\frac{n^2}{(n%2B1)^2}$ and $\frac{n}{n%2B1}$ . So, in all three cases, we have 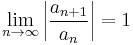$\lim_{n\rightarrow\infty}\left|\frac{a_{n%2B1}}{a_n}\right|=1$ . This illustrates that when L=1, the series may converge or diverge and hence the original ratio test is inconclusive. For the first series 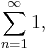$\sum_{n=1}^\infty 1,$ , however, as the term-by-term magnitude ratio 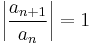$\left|\frac{a_{n%2B1}}{a_n}\right|=1$ for all n, we can apply the third criterion in the refined version of the ratio test to conclude that the series diverges.

Proof

Below is a proof of the validity of the original ratio test.

Suppose that 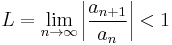$L = \lim_{n\rightarrow\infty} \left| \frac{a_{n%2B1}}{a_{n}}\right| < 1$ . We can then show that the series converges absolutely by showing that its terms will eventually become less than those of a certain convergent geometric series. To do this, let 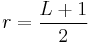$r = \frac{L%2B1}{2}$ . Then r is strictly between L and 1, and 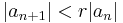$|a_{n%2B1}| < r |a_{n}|$ for sufficiently large n (say, n greater than N). Hence 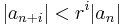$|a_{n%2Bi}| < r^i|a_{n}|$ for each n > N and i > 0, and so

$\sum_{i=N%2B1}^{\infty}|a_{i}| = \sum_{i=1}^{\infty}|a_{N%2Bi}| < \sum_{i=1}^{\infty}r^{i}|a_{N%2B1}| = |a_{N%2B1}|\sum_{i=1}^{\infty}r^{i} = |a_{N%2B1}|\frac{r}{1 - r} < \infty.$

That is, the series converges absolutely.

On the other hand, if L > 1, then 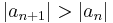$|a_{n%2B1}| > |a_{n}|$ for sufficiently large n, so that the limit of the summands is non-zero. Hence the series diverges.

Extensions for L=1

As seen in the previous example, the ratio test may be inconclusive when the limit of the ratio is 1. Extensions to ratio test, however, sometimes allows one to deal with this case. For instance, the aforementioned refined version of the test handles the case 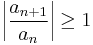$\left|\frac{a_{n%2B1}}{a_n}\right|\ge1$ . Below are some other extensions.

Raabe's test

This extension is due to Joseph Ludwig Raabe. It states that if

$\lim_{n\rightarrow\infty}\left|\frac{a_{n%2B1}}{a_n}\right|=1$

and if

$\lim_{n\rightarrow\infty} \,n\left(\,\left|\frac{a_{n%2B1}}{a_n}\right|-1\right)<-1$

then the series will be absolutely convergent. d'Alembert's ratio test and Raabe's test are the first and second theorem in a hierarchy of such theorems due to Augustus De Morgan.

Higher order tests

The next cases in de Morgan's hierarchy are Bertrand's and Gauss's test. Each test involves slightly different higher order asymptotics. If

$\left|\frac{a_n}{a_{n%2B1}}\right| = 1 %2B \frac{1}{n} %2B \frac{\rho_n}{n\ln n}$

then the series converges if lim inf ρ_n > 1, and diverges if lim sup ρ_n < 1. This is Bertrand's test.

$\left|\frac{a_n}{a_{n%2B1}}\right| = 1%2B \frac{h}{n} %2B \frac{C_n}{n^r}$

where r > 1 and C_n is bounded, then the series converges if h > 1 and diverges if h ≤ 1. This is Gauss's test.

These are both special cases of Kummer's test for the convergence of the series Σa_n. Let ζ_n be an auxiliary sequence of positive constants. Let

$\rho = \lim_{n\to\infty} \left(\zeta_n \frac{a_n}{a_{n%2B1}} - \zeta_{n%2B1}\right).$

Then if ρ > 0, the series converges. If ρ < 0 and Σ1/ζ_n diverges, then the series diverges. Otherwise the test is inconclusive.

Footnotes

^ Rudin 1976, §3.34
^ Apostol 1974, §8.14

References

d'Alembert, J. (1768), Opuscules, V, pp. 171–183, http://gallica.bnf.fr/ark:/12148/bpt6k62424s.image.f192 .

Apostol, Tom M. (1974), Mathematical analysis (2nd ed.), Addison-Wesley, ISBN 978-0-201-00288-1 : §8.14.

Knopp, Konrad (1956), Infinite Sequences and Series, New York: Dover publications, Inc., ISBN 0-486-60153-6 : §3.3, 5.4.

Rudin, Walter (1976), Principles of Mathematical Analysis (3rd ed.), New York: McGraw-Hill, Inc., ISBN 0-07-054235-X : §3.34.

Weisstein, Eric W., "Bertrand's Test" from MathWorld.

Weisstein, Eric W., "Gauss's Test" from MathWorld.

Weisstein, Eric W., "Kummer's Test" from MathWorld.

Watson, G. N.; Whittaker, E. T. (1963), A Course in Modern Analysis (4th ed.), Cambridge University Press, ISBN 0-521-58807-3 : §2.36, 2.37.