Rarita–Schwinger equation

In theoretical physics, the Rarita–Schwinger equation is the relativistic field equation of spin-3/2 fermions. It is similar to the Dirac equation for spin-1/2 fermions. This equation was first introduced by William Rarita and Julian Schwinger in 1941. In modern notation it can be written as^[1]:

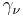$\left ( \epsilon^{\mu \nu \rho \sigma} \gamma_5 \gamma_\nu \partial_\rho %2B m \sigma^{\mu \sigma} \right)\psi_\sigma = 0$

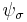where $\epsilon^{\mu \nu \rho \sigma}$ is the Levi-Civita symbol, $\gamma_5$ and $\gamma_\nu$ are Dirac matrices, $m$ is the mass, $\sigma^{\mu \nu} \equiv i/2\left [ \gamma^\mu , \gamma^\nu \right ]$ , and $\psi_\sigma$ is a vector-valued spinor with additional components compared to the four component spinor in the Dirac equation. It corresponds to the 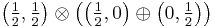$\left(\tfrac{1}{2},\tfrac{1}{2}\right)\otimes \left(\left(\tfrac{1}{2},0\right)\oplus \left(0,\tfrac{1}{2}\right)\right)$ representation of the Lorentz group, or rather, its $\left(1,\tfrac{1}{2}\right) \oplus \left(\tfrac{1}{2},1 \right)$ part^[2]. This field equation can be derived as the Euler–Lagrange equation corresponding to the Rarita-Schwinger Lagrangian^[3]:

$\mathcal{L}=-\tfrac{i}{2}\;\bar{\psi}_\mu \left ( \epsilon^{\mu \nu \rho \sigma} \gamma_5 \gamma_\nu \partial_\rho %2B m \sigma^{\mu \sigma} \right)\psi_\sigma$

where the bar above 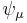$\psi_\mu$ denotes the Dirac adjoint.

This equation is useful for the wave function of composite objects like (N), Delta (Δ)(Δ) baryons or for the hypothetical gravitino. So far, no fundamental particle with spin 3/2 has been found experimentally.

The massless Rarita–Schwinger equation has a gauge symmetry, under the gauge transformation of 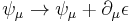$\psi_\mu \rightarrow \psi_\mu %2B \partial_\mu \epsilon$ , where 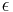$\mathcal{\epsilon}$ is an arbitrary spinor field.

"Weyl" and "Majorana" versions of the Rarita–Schwinger equation also exist.

Drawbacks of the equation

The current description of massive, higher spin fields through either Rarita-Schwinger or Fierz-Pauli formalisms is afflicted with several maladies. As in the case of the Dirac equation, electromagnetic interaction can be added by promoting the partial derivative to gauge covariant derivative:

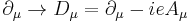$\partial_\mu \rightarrow D_\mu = \partial_\mu - i e A_\mu$ .

In 1969, Velo and Zwanziger showed that the Rarita–Schwinger lagrangian coupled to electromagnetism leads to equation with solutions representing wavefronts, some of which propagate faster than light. In other words, the field then suffers from acausal, superluminal propagation; consequently, the quantization in interaction with electromagnetism is essentially flawed.

Notes

W. Rarita and J. Schwinger, On a Theory of Particles with Half-Integral Spin Phys. Rev. 60, 61 (1941).
Collins P.D.B., Martin A.D., Squires E.J., Particle physics and cosmology (1989) Wiley, Section 1.6.
G. Velo, D. Zwanziger, Propagation and Quantization of Rarita-Schwinger Waves in an External Electromagnetic Potential, Phys. Rev. 186, 1337 (1969).
G. Velo, D. Zwanziger, Noncausality and Other Defects of Interaction Lagrangians for Particles with Spin One and Higher, Phys. Rev. 188, 2218 (1969).
M. Kobayashi, A. Shamaly, Minimal Electromagnetic coupling for massive spin-two fields, Phys. Rev. D 17,8, 2179 (1978).

References

^ S. Weinberg, "The quantum theory of fields", Vol. 3, Cambridge p. 335
^ S. Weinberg, "The quantum theory of fields", Vol. 1, Cambridge p. 232
^ S. Weinberg, "The quantum theory of fields", Vol. 3, Cambridge p. 335