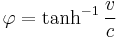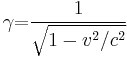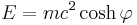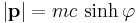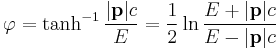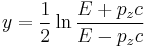Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities (say, in one-dimensional space) rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The rapidity of light is infinite. Rapidity can also link geometric techniques to Minkowski diagrams. The rapidity concept is not widely (nor fashionably) used; speed has the advantage of more direct measurability.
Contents[hide] |
Detail
The rapidity φ of an object relative to a frame of reference is the hyperbolic angle defined as
where
- v is the speed of the object relative to the same frame of reference,
- c is the speed of light, and
- tanh−1 is the inverse hyperbolic tangent function.
For low speeds, φ is approximately v/c.
In 1910 E.T. Whittaker used this parameter in his description of the development of the Lorentz transformation in the first edition of his History of the Theories of Aether and Electricity. [1]
The rapidity parameter was named in 1911 by Alfred Robb; his term was acknowledged by Varićak (1912), Silberstein (1914), Eddington (1924), Morley (1936) and Rindler (2001).
In one spatial dimension
The rapidity φ arises in the linear representation of a Lorentz boost as a vector-matrix product
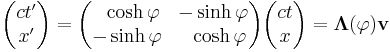 .
.
The matrix Λ(φ) is of the type 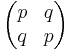 with p and q satisfying
with p and q satisfying 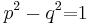 . The study of all matrices
. The study of all matrices 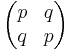 with p, q ∈ R is taken up in the article split-complex number. It is not hard to prove that
with p, q ∈ R is taken up in the article split-complex number. It is not hard to prove that
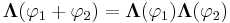 .
.
This establishes the useful additive property of rapidity: if 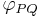 denotes the rapidity of Q relative to P, then
denotes the rapidity of Q relative to P, then
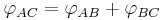 ,
,
provided A, B and C all lie on the same straight line. The simplicity of this formula contrasts with the complexity of the corresponding velocity-addition formula. The simple formula (as well as the matrix above) is analogous to a formula for adding angles of two ordinary rotations in the Euclidean space (and for a rotation matrix): indeed, rapidity may be understood as a "hyperbolic angle" or a Minkowskian counterpart of an angle.
The exponential function, logarithm, sinh, cosh, and tanh are all transcendental functions, requiring methods beyond algebraic expression. Conservatism in physical science explains the reluctance to rely on these functions in some presentations of relativity physics (see Scott Walter (1999)). Nevertheless, the Lorentz factor
identifies with 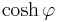 where φ is rapidity. So the hyperbolic angle φ is implicit in the Lorentz transformation expressions using γ and β.
where φ is rapidity. So the hyperbolic angle φ is implicit in the Lorentz transformation expressions using γ and β.
Mathematically, the rapidity can be viewed as a re-linearization of the speed, since the naively linear v becomes absurd as v approaches c.
Proper acceleration (the acceleration 'felt' by the object being accelerated) is the rate of change of rapidity with respect to proper time (time as measured by the object undergoing acceleration itself). Therefore the rapidity of an object in a given frame can be viewed simply as the velocity of that object as would be calculated non-relativistically by an inertial guidance system on board the object itself if it accelerated from rest in that frame to its given speed.
In more than one spatial dimension
From mathematical point of view, possible values of relativistic velocity form a manifold, where the metric tensor corresponds to the proper acceleration (see above). This is a non-flat space (namely, a hyperbolic space), and rapidity is just the distance from the given velocity to the zero velocity in given frame of reference. Although it is possible, as noted above, to add and subtract rapidities where corresponding relative velocities are parallel, in general case the rapidity-addition formula is more complex because of negative curvature. For example, the result of "addition" of two perpendicular motions with rapidities φ1 and φ2 will be greater than 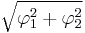 expected by Pythagorean theorem. Rapidity in two dimensions can be usefully visualized using the Poincare disk.[2] Points at the edge of the disk correspond to infinite rapidity. Geodesics correspond to steady accelerations. The Thomas precession is equal to minus the angular deficit of a triangle, or to minus the area of the triangle.
expected by Pythagorean theorem. Rapidity in two dimensions can be usefully visualized using the Poincare disk.[2] Points at the edge of the disk correspond to infinite rapidity. Geodesics correspond to steady accelerations. The Thomas precession is equal to minus the angular deficit of a triangle, or to minus the area of the triangle.
In experimental particle physics
The energy E and scalar momentum |p| of a particle of non-zero (rest) mass m are given by
and so rapidity can be calculated from measured energy and momentum by
However, experimental particle physicists often use a modified definition of rapidity relative to a beam axis
where 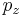 is the component of momentum along the beam axis.[3] This is the rapidity of the boost along the beam axis which takes an observer from the lab frame to a frame in which the particle moves only perpendicular to the beam. Related to this is the concept of pseudorapidity.
is the component of momentum along the beam axis.[3] This is the rapidity of the boost along the beam axis which takes an observer from the lab frame to a frame in which the particle moves only perpendicular to the beam. Related to this is the concept of pseudorapidity.
References
- ^ Whittaker (1910) A History of the theories of aether and electricity (1. edition), page 441, Dublin: Longman, Green and Co. In 1953 when he published the second volume of the second edition of the History, the use of the rapidity parameter is found on page 32.
- ^ http://www.bates.edu/%7Emsemon/RhodesSemonFinal.pdf
- ^ Amsler, C. et al., "The Review of Particle Physics", Physics Letters B 667 (2008) 1, Section 38.5.2
- Arthur Stanley Eddington (1924) The Mathematical Theory of Relativity, 2nd edition, Cambridge University Press, p.22.
- Frank Morley (1936) "When and Where", The Criterion, edited by T.S. Eliot, 15:200-2009.
- Vladimir Karapetoff (1936) "Restricted relativity in terms of hyperbolic functions of rapidities", American Mathematical Monthly 43:70.
- Wolfgang Rindler (2001) Relativity: Special, General, and Cosmological, page 53, Oxford University Press.
- Robb, Alfred (1911). Optical geometry of motion, a new view of the theory of relativity. Cambridge: Heffner & Sons. http://www.archive.org/details/opticalgeometryo00robbrich.
- Silberstein, Ludwik (1914). The Theory of Relativity. London: Macmillan & Co.. http://www.archive.org/details/theoryofrelativi00silbrich.
- Walter, Scott (1999). "The non-Euclidean style of Minkowskian relativity". In J. Gray. The Symbolic Universe: Geometry and Physics. Oxford University Press. pp. 91–127. http://www.univ-nancy2.fr/DepPhilo/walter/papers/nes.pdf.(see page 17 of e-link)
- Whittaker, E.T. (1910). 1. Edition: A History of the theories of aether and electricity. Dublin: Longman, Green and Co..