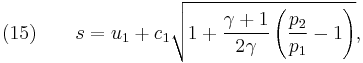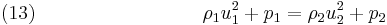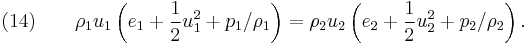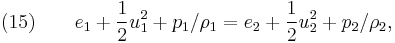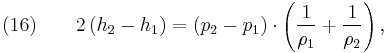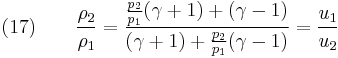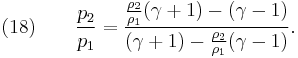Rankine–Hugoniot conditions
The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, relate to the behaviour of shock waves traveling normal to the prevailing flow. They are named in recognition of the work carried out by Scottish engineer and physicist William John Macquorn Rankine[1] and French engineer Pierre Henri Hugoniot.[2] See also Salas (2006)[3] for some historical background.
Contents |
Introduction
Consider a one-dimensional, calorically ideal gas described by a polytropic equation-of-state and operating under adiabatic conditions. In addition, assume that the fluid is inviscid (negligible viscosity effects). Such a system can be described by the following system of conservation laws, known as the 1D Euler equations
where,
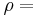 fluid mass density, [kg/m3]
fluid mass density, [kg/m3]
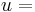 fluid velocity, [m/s]
fluid velocity, [m/s]
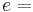 fluid-specific internal energy, [J/kg]
fluid-specific internal energy, [J/kg]
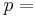 fluid pressure, [Pa]
fluid pressure, [Pa]
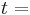 time, [s]
time, [s]
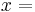 distance, [m], and
distance, [m], and
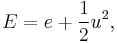 fluid-specific total energy, [J/kg].
fluid-specific total energy, [J/kg].
For adiabatic conditions a polytropic process can be represented by the equation-of-state,
where  represents the polytropic exponent (equal to the ratio of specific heats
represents the polytropic exponent (equal to the ratio of specific heats 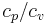 ) of the polytropic process
) of the polytropic process
For an extensive list of compressible flow equations, etc., refer to NACA Report 1135 (1953).[4]
Note: For a calorically ideal gas 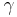 is a constant and for a thermally ideal gas
is a constant and for a thermally ideal gas 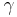 is a function of temperature.
is a function of temperature.
The jump condition
Before proceeding further it is necessary to introduce the concept of a jump condition – a condition that holds at a discontinuity or abrupt change.
Consider a 1D situation where there is a jump in the scalar conserved physical quantity  , which is governed by the hyperbolic conservation law
, which is governed by the hyperbolic conservation law
Let the solution exhibit a jump (or shock) at 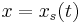 and integrate over the partial domain,
and integrate over the partial domain, 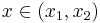 , where
, where 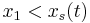 and
and 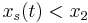 ,
,
The subscripts 1 and 2 indicate conditions just upstream and just downstream of the jump respectively. Note, to arrive at equation (8) we have used the fact that 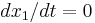 and
and 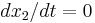 .
.
Now, let 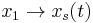 and
and 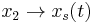 , when we have
, when we have 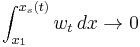 and
and 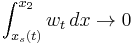 , and in the limit
, and in the limit
where we have defined 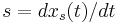 (the system characteristic or shock speed), which by simple division is given by
(the system characteristic or shock speed), which by simple division is given by
Equation (9) represents the jump condition for conservation equation (6). A shock situation arises in a system where its characteristics intersect, and under these conditions a requirement for a unique single-valued solution is that the solution should satisfy the admissibility condition or entropy condition. For physically real applications this means that the solution should satisfy the Lax entropy condition
where 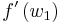 and
and 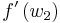 represent characteristic speeds at upstream and downstream conditions respectively.
represent characteristic speeds at upstream and downstream conditions respectively.
Euler equations shock condition
In the case of the hyperbolic conservation equation (6), we have seen that the shock speed can be obtained by simple division. However, for the 1D Euler equations ( 1), ( 2) and ( 3), we have the vector state variable ![\left[\rho,\rho u,\rho E\right]^T](/2012-wikipedia_en_all_nopic_01_2012/I/33ff965b14b4633996c561cdeab09303.png) and the jump conditions become
and the jump conditions become
Equations (12), (13) and (14) are known as the Rankine–Hugoniot conditions for the Euler equations and are derived by enforcing the conservation laws in integral form over a control volume that includes the shock. For this situation  cannot be obtained by simple division. However, it can be shown by transforming the problem to a moving co-ordinate system, i.e.
cannot be obtained by simple division. However, it can be shown by transforming the problem to a moving co-ordinate system, i.e. 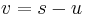 , and some algebraic manipulation, that the shock speed is given by
, and some algebraic manipulation, that the shock speed is given by
where 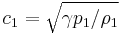 is the speed of sound in the fluid at upstream conditions.
is the speed of sound in the fluid at upstream conditions.
See Laney (1998),[5] LeVeque (2002),[6] Toro (1999),[7] Wesseling (2001),[8] and Whitham (1999)[9] for further discussion.
Stationary shock
For a stationary shock 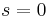 , and for the 1D Euler equations we have
, and for the 1D Euler equations we have
In view of equation (12) we can simplify equation (14) to
which is a statement of Bernoulli's principle, under conditions where gravitational effects can be neglected.
Substituting 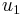 and
and 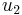 from equations (12) and (13) into equation (15) yields the following relationship:
from equations (12) and (13) into equation (15) yields the following relationship:
where 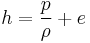 represents specific enthalpy of the fluid. Eliminating internal energy
represents specific enthalpy of the fluid. Eliminating internal energy  in equation (15) by use of the equation-of-state, equation ( 4), yields
in equation (15) by use of the equation-of-state, equation ( 4), yields
From physical considerations it is clear that both the upstream and downstream pressures must be positive, and this imposes an upper limit on the density ratio in equations (17) and (18) such that 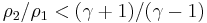 . As the strength of the shock increases, there is a corresponding increase in downstream gas temperature, but the density ratio
. As the strength of the shock increases, there is a corresponding increase in downstream gas temperature, but the density ratio 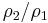 approaches a finite limit: 4 for an ideal monatomic gas
approaches a finite limit: 4 for an ideal monatomic gas 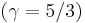 and 6 for an ideal diatomic gas
and 6 for an ideal diatomic gas 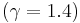 . Note: air is comprised predominately of diatomic molecules and therefore at standard conditions
. Note: air is comprised predominately of diatomic molecules and therefore at standard conditions 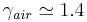 .
.
See also
- Calculate normal shock wave parameters for mixtures of imperfect gases. Gas Dynamics Toolbox
- Shock polar
References
- ^ Rankine, W. J. M. (1870). "On the thermodynamic theory of waves of finite longitudinal disturbances". Phil. Trans. Roy. Soc. 160: 277. doi:10.1098/rstl.1870.0015. http://gallica.bnf.fr/scripts/get_page.exe?O=55965&E=328&N=11&CD=1&F=PDF.
- ^ Hugoniot, H. (1887). "Propagation des Mouvements dans les Corps et spécialement dans les Gaz Parfaits" (in French). Journal de l'Ecole Polytechnique 57: 3.
- ^ Salas, M. D. (2006). "The Curious Events Leading to the Theory of Shock Waves, Invited lecture, 17th Shock Interaction Symposium, Rome, 4–8 September.". http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20060047586_2006228914.pdf.
- ^ Ames Research Staff (1953), "Equations, Tables and Charts for Compressible Flow", Report 1135 of the National Advisory Committee for Aeronautics, http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930091059_1993091059.pdf
- ^ Laney, Culbert B. (1998). Computational Gasdynamics. Cambridge University Press. ISBN 978-0521625586.
- ^ LeVeque, Randall (2002). Finite Volume Methods for Hyperbolic Problems. Cambridge University Press. ISBN 978-0521009249.
- ^ Toro, E. F. (1999). Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer-Verlag. ISBN 978-3540659662.
- ^ Wesseling, Pieter (2001). Principles of Computational Fluid Dynamics. Springer-Verlag. ISBN 978-3540678533.
- ^ Whitham, G. B. (1999). Linear and Nonlinear Waves. Wiley. ISBN 978-0471940906.
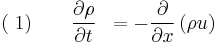
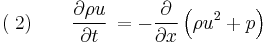
![(\;3)\quad \quad\frac{\partial\rho E}{\partial t} = -\frac{\partial}{\partial x}\left[\rho u\left(e%2B\frac{1}{2}u^{2}%2Bp/\rho\right)\right],](/2012-wikipedia_en_all_nopic_01_2012/I/0cbb99f072f996cd17325d3d9dd11f6e.png)
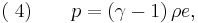
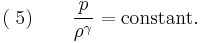
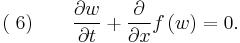
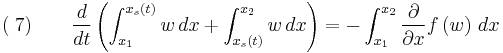

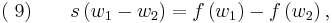
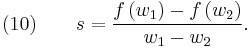
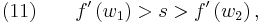
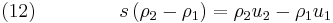
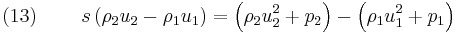
![(14)\quad\quad s\left(\rho_2 E_2 - \rho_1 E_1 \right) = \left[ \rho_ 2 u_ 2 \left( e_ 2 %2B \frac{1}{2} u_2^2 %2Bp_2/\rho_2 \right)\right] - \left[\rho_1 u_1 \left( e_1 %2B \frac{1}{2} u_1^2 %2B p_1/\rho_1 \right)\right].](/2012-wikipedia_en_all_nopic_01_2012/I/abf6a0969a7fd201a90dafac0a234c4e.png)