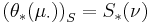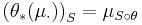Radonifying function
In measure theory, a radonifying function (ultimately named after Johann Radon) between measurable spaces is one that takes a cylinder set measure (CSM) on the first space to a true measure on the second space. It acquired its name because the pushforward measure on the second space was historically thought of as a Radon measure.
Definition
Given two separable Banach spaces  and
and  , a CSM
, a CSM 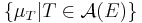 on
on  and a continuous linear map
and a continuous linear map 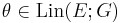 , we say that
, we say that  is radonifying if the push forward CSM (see below)
is radonifying if the push forward CSM (see below) 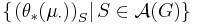 on
on  "is" a measure, i.e. there is a measure
"is" a measure, i.e. there is a measure  on
on  such that
such that
for each 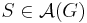 , where
, where 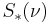 is the usual push forward of the measure
is the usual push forward of the measure  by the linear map
by the linear map 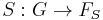 .
.
Push forward of a CSM
Because the definition of a CSM on  requires that the maps in
requires that the maps in 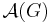 be surjective, the definition of the push forward for a CSM requires careful attention. The CSM
be surjective, the definition of the push forward for a CSM requires careful attention. The CSM
is defined by
if the composition 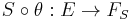 is surjective. If
is surjective. If 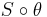 is not surjective, let
is not surjective, let 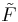 be the image of
be the image of 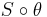 , let
, let 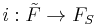 be the inclusion map, and define
be the inclusion map, and define
-
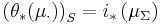 ,
,
where 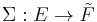 (so
(so 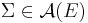 ) is such that
) is such that 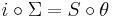 .
.