R-algebroid

In mathematics, R-algebroids are constructed starting from groupoids. These are more abstract concepts than the Lie algebroids that play a similar role in the theory of Lie groupoids to that of Lie algebras in the theory of Lie groups. (Thus, a Lie algebroid can be thought of as 'a Lie algebra with many objects ').

1 Definition
2 R-category
3 R-algebroids via convolution products
4 Examples
5 Notes
6 References
7 See also

Definition

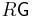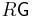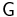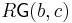An R-algebroid, $R\mathsf{G}$ , is constructed as follows. The object set of $R\mathsf{G}$ is the same as that of $\mathsf{G}$ and $R\mathsf{G}(b,c)$ is the free R-module on the set 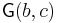$\mathsf{G}(b,c)$ , with composition given by the usual bilinear rule, extending the composition of 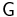$\mathsf{G}$ ^[1].

R-category

More generally, an R-category is defined as an extension of this R-algebroid concept by replacing the groupoid 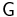$\mathsf{G}$ in this construction with a general category C (that does not have all morphisms invertible).

R-algebroids via convolution products

One can also define the R-algebroid, 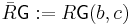${\bar R}\mathsf{G}:=R\mathsf{G}(b,c)$ , to be the set of functions 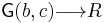$\mathsf{G}(b,c){\longrightarrow}R$ with finite support, and with the convolution product defined as follows: 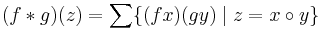$\displaystyle (f*g)(z)= \sum \{(fx)(gy)\mid z=x\circ y \}$ .^[2]

Only this second construction is natural for the topological case, when one needs to replace 'function' by 'continuous function with compact support', and in this case 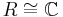$R\cong \mathbb{C}$ .

Examples

Every Lie algebra is a Lie algebroid over the one point manifold.
The Lie algebroid associated to a Lie groupoid.

Notes

^ G. H. Mosa: Higher dimensional algebroids and Crossed complexes, PhD Thesis, University of Wales, Bangor, (1986). (supervised by Ronald Brown)
^ R. Brown and G. H. Mosa. Double algebroids and crossed modules of algebroids, University of Wales-Bangor, Maths Preprint, 1986.

This article incorporates material from Algebroid Structures and Algebroid Extended Symmetries, which is licensed under the Creative Commons Attribution/Share-Alike License.

References

R. Brown and G. H. Mosa. Double algebroids and crossed modules of algebroids, University of Wales-Bangor, Maths Preprint, 1986.

G. H. Mosa: Higher dimensional algebroids and Crossed complexes, PhD Thesis, University of Wales, Bangor, (1986). (supervised by Ronald Brown).

Kirill Mackenzie, Lie Groupoids and Lie Algebroids in Differential Geometry, Cambridge U. Press, 1987.

Kirill Mackenzie, General Theory of Lie Groupoids and Lie Algebroids, Cambridge U. Press, 2005

Charles-Michel Marle, Differential calculus on a Lie algebroid and Poisson manifolds (2002). Also available in arXiv:0804.2451

Alan Weinstein, Groupoids: unifying internal and external symmetry, AMS Notices, 43 (1996), 744-752. Also available as arXiv:math/9602220