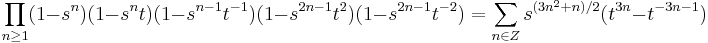Quintuple product identity
In mathematics the Watson quintuple product identity is an infinite product identity introduced by Watson (1929) and rediscovered by Bailey (1951) and Gordon (1961). It is analogous to the Jacobi triple product identity, and is the Macdonald identity for a certain non-reduced affine root system.
Statement
References
- Bailey, W. N. (1951), "On the simplification of some identities of the Rogers-Ramanujan type", Proceedings of the London Mathematical Society. Third Series 1: 217–221, doi:10.1112/plms/s3-1.1.217, ISSN 0024-6115, MR0043839
- Carlitz, L.; Subbarao, M. V. (1972), "A simple proof of the quintuple product identity", Proceedings of the American Mathematical Society 32: 42–44, ISSN 0002-9939, JSTOR 2038301, MR0289316
- Gordon, Basil (1961), "Some identities in combinatorial analysis", The Quarterly Journal of Mathematics. Oxford. Second Series 12: 285–290, ISSN 0033-5606, MR0136551
- Watson, G. N. (1929), "Theorems stated by Ramanujan. VII: Theorems on continued fractions.", Journal of the London Mathematical Society 4 (1): 39–48, doi:10.1112/jlms/s1-4.1.39, ISSN 0024-6107, JFM 55.0273.01