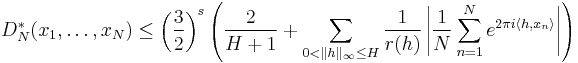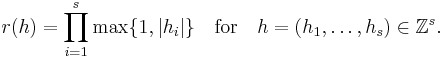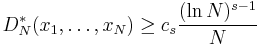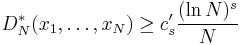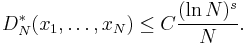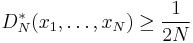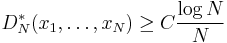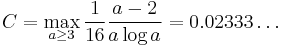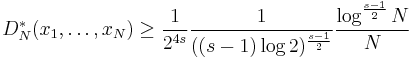Low-discrepancy sequence
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy.
Roughly speaking, the discrepancy of a sequence is low if the number of points in the sequence falling into an arbitrary set B is close to proportional to the measure of B, as would happen on average (but not for particular samples) in the case of a uniform distribution. Specific definitions of discrepancy differ regarding the choice of B (hyperspheres, hypercubes, etc.) and how the discrepancy for every B is computed (usually normalized) and combined (usually by taking the worst value).
Low-discrepancy sequences are also called quasi-random or sub-random sequences, due to their common use as a replacement of uniformly distributed random numbers. The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence are neither random nor pseudorandom, but such sequences share some properties of random variables and in certain applications such as the quasi-Monte Carlo method their lower discrepancy is an important advantage.
At least three methods of numerical integration can be phrased as follows. Given a set {x1, ..., xN} in the interval [0,1], approximate the integral of a function f as the average of the function evaluated at those points:
If the points are chosen as xi = i/N, this is the rectangle rule. If the points are chosen to be randomly (or pseudorandomly) distributed, this is the Monte Carlo method. If the points are chosen as elements of a low-discrepancy sequence, this is the quasi-Monte Carlo method. A remarkable result, the Koksma–Hlawka inequality (stated below), shows that the error of such a method can be bounded by the product of two terms, one of which depends only on f, and the other one is the discrepancy of the set {x1, ..., xN}.
It is convenient to construct the set {x1, ..., xN} in such a way that if a set with N+1 elements is constructed, the previous N elements need not be recomputed. The rectangle rule uses points set which have low discrepancy, but in general the elements must be recomputed if N is increased. Elements need not be recomputed in the Monte Carlo method if N is increased, but the point sets do not have minimal discrepancy. By using low-discrepancy sequences, the quasi-Monte Carlo method has the desirable features of the other two methods.
Definition of discrepancy
The discrepancy of a set P = {x1, ..., xN} is defined, using Niederreiter's notation, as
where λs is the s-dimensional Lebesgue measure, A(B;P) is the number of points in P that fall into B, and J is the set of s-dimensional intervals or boxes of the form
where 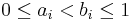 .
.
The star-discrepancy D*N(P) is defined similarly, except that the supremum is taken over the set J* of intervals of the form
where ui is in the half-open interval [0, 1).
The two are related by
Graphical examples
The points plotted below are the first 100, 1000, and 10000 elements in a sequence of the Sobol' type. For comparison, 10000 elements of a sequence of pseudorandom points are also shown. The low-discrepancy sequence was generated by TOMS algorithm 659[1]. An implementation of the algorithm in Fortran is available from Netlib.
The Koksma–Hlawka inequality
Let Īs be the s-dimensional unit cube, Īs = [0, 1] × ... × [0, 1]. Let f have bounded variation V(f) on Īs in the sense of Hardy and Krause. Then for any x1, ..., xN in Is = [0, 1) × ... × [0, 1),
The Koksma-Hlawka inequality is sharp in the following sense: For any point set {x1,...,xN} in Is and any 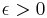 , there is a function f with bounded variation and V(f)=1 such that
, there is a function f with bounded variation and V(f)=1 such that
Therefore, the quality of a numerical integration rule depends only on the discrepancy D*N(x1,...,xN).
The formula of Hlawka-Zaremba
Let 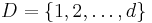 . For
. For 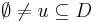 we write
we write
and denote by 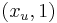 the point obtained from x by replacing the coordinates not in u by
the point obtained from x by replacing the coordinates not in u by 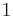 . Then
. Then
The 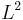 version of the Koksma–Hlawka inequality
version of the Koksma–Hlawka inequality
Applying the Cauchy-Schwarz inequality for integrals and sums to the Hlawka-Zaremba identity, we obtain an 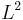 version of the Koksma–Hlawka inequality:
version of the Koksma–Hlawka inequality:
where
and
The Erdős–Turan–Koksma inequality
It is computationally hard to find the exact value of the discrepancy of large point sets. The Erdős–Turán–Koksma inequality provides an upper bound.
Let x1,...,xN be points in Is and H be an arbitrary positive integer. Then
where
The main conjectures
Conjecture 1. There is a constant cs depending only on the dimension s, such that
for any finite point set {x1,...,xN}.
Conjecture 2. There is a constant c's depending only on s, such that
for any infinite sequence x1,x2,x3,....
These conjectures are equivalent. They have been proved for s ≤ 2 by W. M. Schmidt. In higher dimensions, the corresponding problem is still open. The best-known lower bounds are due to K. F. Roth.
The best-known sequences
Constructions of sequences are known such that
where C is a certain constant, depending on the sequence. After Conjecture 2, these sequences are believed to have the best possible order of convergence. See also: van der Corput sequence, Halton sequences, Sobol sequences.
Lower bounds
Let s = 1. Then
for any finite point set {x1, ..., xN}.
Let s = 2. W. M. Schmidt proved that for any finite point set {x1, ..., xN},
where
For arbitrary dimensions s > 1, K.F. Roth proved that
for any finite point set {x1, ..., xN}. This bound is the best known for s > 3.
Applications
References
- Kuipers, L.; Niederreiter, H. (2005), Uniform distribution of sequences, Dover Publications, ISBN 0-486-45019-8
- Harald Niederreiter. Random Number Generation and Quasi-Monte Carlo Methods. Society for Industrial and Applied Mathematics, 1992. ISBN 0-89871-295-5
- Michael Drmota and Robert F. Tichy, Sequences, discrepancies and applications, Lecture Notes in Math., 1651, Springer, Berlin, 1997, ISBN 3-540-62606-9
- William H. Press, Brian P. Flannery, Saul A. Teukolsky, William T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, second edition 1992. ISBN 0-521-43108-5 (see Section 7.7 for a less technical discussion of low-discrepancy sequences)
- Quasi-Monte Carlo Simulations, http://www.puc-rio.br/marco.ind/quasi_mc.html
External links
- Collected Algorithms of the ACM (See algorithms 647, 659, and 738.)
- GNU Scientific Library Quasi-Random Sequences
- ^ P. Bratley and B.L. Fox in ACM Transactions on Mathematical Software, vol. 14, no. 1, pp 88—100
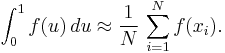
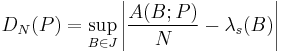
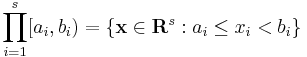
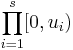
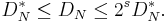
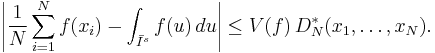
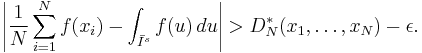
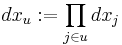
![\frac{1}{N} \sum_{i=1}^N f(x_i)
- \int_{\bar I^s} f(u)\,du=
\sum_{\emptyset\neq u\subseteq D}(-1)^{|u|}
\int_{[0,1]^{|u|}}{\rm disc}(x_u,1)\frac{\partial^{|u|}}{\partial x_u}f(x_u,1) dx_u.](/2012-wikipedia_en_all_nopic_01_2012/I/4b758ba3513a41ee5a0b9fed17eae694.png)
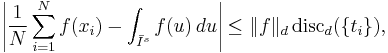
![{\rm disc}_{d}(\{t_i\})=\left(\sum_{\emptyset\neq u\subseteq D}
\int_{[0,1]^{|u|}}{\rm disc}(x_u,1)^2 dx_u\right)^{1/2}](/2012-wikipedia_en_all_nopic_01_2012/I/10cc128f622efcd55660fba9fa8da06b.png)
![\|f\|_{d}=\left(\sum_{u\subseteq D}
\int_{[0,1]^{|u|}}
\left|\frac{\partial^{|u|}}{\partial x_u}f(x_u,1)\right|^2 dx_u\right)^{1/2}.](/2012-wikipedia_en_all_nopic_01_2012/I/f7f03d4caf9c2de0e11a0809171a9d15.png)