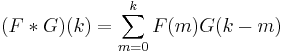Quasi-polynomial
For quasi-polynomial time complexity of algorithms, see Quasi-polynomial time.
In mathematics, a quasi-polynomial (pseudo-polynomial) is a generalization of polynomials. While the coefficients of a polynomial come from a ring, the coefficients of quasi-polynomials are instead periodic functions with integral period. Quasi-polynomials appear throughout much of combinatorics as the enumerators for various objects.
A quasi-polynomial can be written as 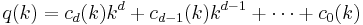 , where
, where 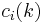 is a periodic function with integral period. If
is a periodic function with integral period. If 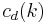 is not identically zero, then the degree of q is d. Equivalently, a function
is not identically zero, then the degree of q is d. Equivalently, a function 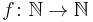 is a quasi-polynomial if there exist polynomials
is a quasi-polynomial if there exist polynomials 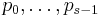 such that
such that  when
when 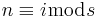 . The polynomials
. The polynomials 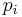 are called the constituents of f.
are called the constituents of f.
Examples
- Given a d-dimensional polytope P with rational vertices
 , define tP to be the convex hull of
, define tP to be the convex hull of 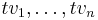 . The function
. The function 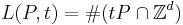 is a quasi-polynomial in t of degree d. In this case, L(P,t) is a function
is a quasi-polynomial in t of degree d. In this case, L(P,t) is a function 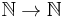 . This is known as the Ehrhart quasi-polynomial, named after Eugène Ehrhart.
. This is known as the Ehrhart quasi-polynomial, named after Eugène Ehrhart. - Given two quasi-polynomials F and G, the convolution of F and G is
which is a quasi-polynomial with degree 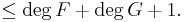
See also
References
- Stanley, Richard P. (1997). Enumerative Combinatorics, Volume 1. Cambridge University Press. ISBN 0-521-55309-1, 0-521-56069-1.