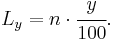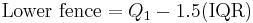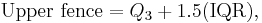Quartile

In descriptive statistics, the quartiles of a set of values are the three points that divide the data set into four equal groups, each representing a fourth of the population being sampled. A quartile is a type of quantile.

In epidemiology, sociology and finance, the quartiles of a population are the four subpopulations defined by classifying individuals according to whether the value concerned falls into one of the four ranges defined by the three values discussed above. Thus an individual item might be described as being "in the upper quartile".

Contents

Definitions

The difference between the upper and lower quartiles is called the interquartile range.

Computing methods

There is no universal agreement on choosing the quartile values.[1]

One standard formula for locating the position of the observation at a given percentile, y, with n data points sorted in ascending order is:[2]

L_y = n \cdot \cfrac{y}{100}.

Example

Method 1

  1. Use the median to divide the ordered data set into two halves. Do not include the median into the halves, or the minimum and maximum.
  2. The lower quartile value is the median of the lower half of the data. The upper quartile value is the median of the upper half of the data.

This rule is employed by the TI-83 calculator boxplot and "1-Var Stats" functions.

Method 2

  1. Use the median to divide the ordered data set into two halves. If the median is a datum (as opposed to being the average of the middle two data), include the median in both halves.
  2. The lower quartile value is the median of the lower half of the data. The upper quartile value is the median of the upper half of the data.

Example 1

Data Set: 6, 47, 49, 15, 42, 41, 7, 39, 43, 40, 36
Ordered Data Set: 6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49

Method 1 Method 2
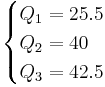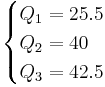\begin{cases} Q_1 = 25.5 \\ Q_2 = 40 \\ Q_3 = 42.5 \end{cases} \begin{cases} Q_1 = 25.5 \\ Q_2 = 40 \\ Q_3 =42.5 \end{cases}

Example 2

Ordered Data Set: 7, 15, 36, 39, 40, 41

Method 1 Method 2
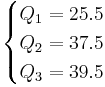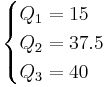\begin{cases} Q_1 = 25.5 \\ Q_2 = 37.5 \\ Q_3 = 39.5 \end{cases} \begin{cases} Q_1 = 15 \\ Q_2 = 37.5 \\ Q_3 = 40 \end{cases}

Outliers

There are methods by which to check for outliers in the discipline of statistics and statistical analysis. As is the basic idea of descriptive statistics, when encountered with an outlier, we have to explain this by further analysis of the cause or origin of the outlier. In cases of extreme observations, which are not an infrequent occurrence, the typical values must be analyzed. In the case of quartiles, the Interquartile Range (IQR) may be used to characterize the data when there may be extremeties that skew the data; the interquartile range is a relatively robust statistic (also sometimes called "resistance") compared to the range and standard deviation. There is also a mathematical method to check for outliers and determining "fences", upper and lower limits from which to check for outliers.

After determining the first and third quartiles and the interquartile range as outlined above, then determining the fences using the following formula:

\text{Lower fence} = Q_1 - 1.5(\mathrm{IQR}) \,
\text{Upper fence} = Q_3 %2B 1.5(\mathrm{IQR}), \,

where Q1 and Q3 are the first and third quartiles, respectively. The Lower fence is the "lower limit" and the Upper fence is the "upper limit" of data, and any data lying outside this defined bounds can be considered an outlier. Anything below the Lower fence or above the Upper fence can be considered such a case. The fences provide a guideline by which to define an outlier, which may be defined in other ways. The fences define a "range" outside of which an outlier exists; a way to picture this is a boundary of a fence, outside of which are "outsiders" as opposed to outliers.

See also

References

  1. ^ Hyndman, Rob J; Fan, Yanan (November 1996). "Sample quantiles in statistical packages". American Statistician 50 (4): 361–365. doi:10.2307/2684934. http://robjhyndman.com/papers/quantiles/. 
  2. ^ McNamara, Timothy J. (2007). Key concepts in mathematics: strengthening standards practice in grades 6–12 (2nd ed.). Corwin Press. ISBN 9781412938426. 

External links