Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. A feature of quaternions is that the product of two quaternions is noncommutative. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space[1] or equivalently as the quotient of two vectors.[2] Quaternions can also be represented as the sum of a scalar and a vector.
Quaternions find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations such as in three-dimensional computer graphics and computer vision. They can be used alongside other methods, such as Euler angles and matrices, or as an alternative to them depending on the application.
In modern language, quaternions form a four-dimensional associative normed division algebra over the real numbers, and thus also form a domain. In fact, the quaternions were the first noncommutative division algebra to be discovered.[3] The algebra of quaternions is often denoted by H (for Hamilton), or in blackboard bold by 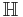 (Unicode U+210D, ℍ). It can also be given by the Clifford algebra classifications Cℓ0,2(R) ≅ Cℓ03,0(R). The algebra H holds a special place in analysis since, according to the Frobenius theorem, it is one of only two finite-dimensional division rings containing the real numbers as a proper subring, the other being the complex numbers.
(Unicode U+210D, ℍ). It can also be given by the Clifford algebra classifications Cℓ0,2(R) ≅ Cℓ03,0(R). The algebra H holds a special place in analysis since, according to the Frobenius theorem, it is one of only two finite-dimensional division rings containing the real numbers as a proper subring, the other being the complex numbers.
The unit quaternions can therefore be thought of as a choice of a group structure on the 3-sphere 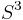 , the group Spin(3), the group SU(2), or the universal cover of SO(3).
, the group Spin(3), the group SU(2), or the universal cover of SO(3).
History
Quaternion algebra was introduced by Irish mathematician Sir William Rowan Hamilton in 1843.[4] Important precursors to this work included Euler's four-square identity (1748) and Olinde Rodrigues' parameterization of general rotations by four parameters (1840), but neither of these writers treated the four-parameter rotations as an algebra.[5][6] Carl Friedrich Gauss had also discovered quaternions in 1819, but this work was only published in 1900.[7]
Hamilton knew that the complex numbers could be interpreted as points in a plane, and he was looking for a way to do the same for points in three-dimensional space. Points in space can be represented by their coordinates, which are triples of numbers, and for many years Hamilton had known how to add and subtract triples of numbers. However, Hamilton had been stuck on the problem of multiplication and division for a long time. He could not figure out how to calculate the quotient of the coordinates of two points in space.
The great breakthrough in quaternions finally came on Monday 16 October 1843 in Dublin, when Hamilton was on his way to the Royal Irish Academy where he was going to preside at a council meeting. While walking along the towpath of the Royal Canal with his wife, the concepts behind quaternions were taking shape in his mind. When the answer dawned on him, Hamilton could not resist the urge to carve the formula for the quaternions
into the stone of Brougham Bridge as he paused on it.
On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Graves, describing the train of thought that led to his discovery. This letter was later published in the London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. xxv (1844), pp 489–95. On the letter, Hamilton states,
And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples ... An electric circuit seemed to close, and a spark flashed forth.
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted most of the remainder of his life to studying and teaching them. He founded a school of "quaternionists", and he tried to popularize quaternions in several books. The last and longest of his books, Elements of Quaternions, was 800 pages long and was published shortly after his death.
After Hamilton's death, his student Peter Tait continued promoting quaternions. At this time, quaternions were a mandatory examination topic in Dublin. Topics in physics and geometry that would now be described using vectors, such as kinematics in space and Maxwell's equations, were described entirely in terms of quaternions. There was even a professional research association, the Quaternion Society, devoted to the study of quaternions and other hypercomplex number systems.
From the mid-1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs, Oliver Heaviside, and Hermann von Helmholtz. Vector analysis described the same phenomena as quaternions, so it borrowed some ideas and terminology liberally from the literature of quaternions. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics and physics. A side-effect of this transition is that Hamilton's work is difficult to comprehend for many modern readers. Hamilton's original definitions are unfamiliar and his writing style was prolix and opaque.
However, quaternions have had a revival since the late 20th Century, primarily due to their utility in describing spatial rotations. The representations of rotations by quaternions are more compact and quicker to compute than the representations by matrices. In addition, unlike Euler angles they are not susceptible to gimbal lock. For this reason, quaternions are used in computer graphics,[8] computer vision, robotics, control theory, signal processing, attitude control, physics, bioinformatics, molecular dynamics, computer simulations, and orbital mechanics. For example, it is common for the attitude-control systems of spacecraft to be commanded in terms of quaternions. Quaternions have received another boost from number theory because of their relationships with the quadratic forms.
Since 1989, the Department of Mathematics of the National University of Ireland, Maynooth has organized a pilgrimage, where scientists (including the physicists Murray Gell-Mann in 2002, Steven Weinberg in 2005, and the mathematician Andrew Wiles in 2003) take a walk from Dunsink Observatory to the Royal Canal bridge where no trace of Hamilton's carving remains, unfortunately.
Definition
As a set, the quaternions H are equal to R4, a four-dimensional vector space over the real numbers. H has three operations: addition, scalar multiplication, and quaternion multiplication. The sum of two elements of H is defined to be their sum as elements of R4. Similarly the product of an element of H by a real number is defined to be the same as the product in R4. To define the product of two elements in H requires a choice of basis for R4. The elements of this basis are customarily denoted as 1, i, j, and k. Every element of H can be uniquely written as a linear combination of these basis elements, that is, as a1 + bi + cj + dk, where a, b, c, and d are real numbers. The basis element 1 will be the identity element of H, meaning that multiplication by 1 does nothing, and for this reason, elements of H are usually written a + bi + cj + dk, suppressing the basis element 1. Given this basis, associative quaternion multiplication is defined by first defining the products of basis elements and then defining all other products using the distributive law.
Multiplication of basis elements
The equations
where i, j, and k are basis elements of H, determine all the possible products of i, j, and k. For example, since
right-multiplying both sides by k gives
All the other possible products can be determined by similar methods, resulting in
which can be arranged as a table whose rows represent the left factor of the product and whose columns represent the right factor:
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
Hamilton product
For two elements a1 + b1i + c1j + d1k and a2 + b2i + c2j + d2k, their Hamilton product (a1 + b1i + c1j + d1k)(a2 + b2i + c2j + d2k) is determined by the products of the basis elements and the distributive law. The distributive law makes it possible to expand the product so that it is a sum of products of basis elements. This gives the following expression:
Now the basis elements can be multiplied using the rules given above to get:[4]
Ordered list form
Using the basis 1, i, j, k of H makes it possible to write H as a set of quadruples:
Then the basis elements are:
and the formulas for addition and multiplication are:
and
Scalar and vector parts
A number of the form a + 0i + 0j + 0k, where a is a real number, is called real, and a number of the form 0 + bi + cj + dk, where b, c, and d are real numbers, and at least one of b, c or d is nonzero, is called pure imaginary. If a + bi + cj + dk is any quaternion, then a is called its scalar part and bi + cj + dk is called its vector part. The scalar part of a quaternion is always real, and the vector part is always pure imaginary. Even though every quaternion is a vector in a four-dimensional vector space, it is common to define a vector to mean a pure imaginary quaternion. With this convention, a vector is the same as an element of the vector space R3.
Hamilton called pure imaginary quaternions right quaternions[9][10] and real numbers (considered as quaternions with zero vector part) scalar quaternions.
If a quaternion is divided up into a scalar part and a vector part, i.e.
then the formulas for addition and multiplication are:
and
where "·" is the dot product and "×" is the cross product.
Remarks
Noncommutative
Unlike multiplication of real or complex numbers, multiplication of quaternions is not commutative: For example, 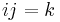 , while
, while 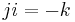 . The noncommutativity of multiplication has some unexpected consequences, among them that polynomial equations over the quaternions can have more distinct solutions than the degree of the polynomial. The equation
. The noncommutativity of multiplication has some unexpected consequences, among them that polynomial equations over the quaternions can have more distinct solutions than the degree of the polynomial. The equation 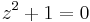 , for instance, has infinitely many quaternion solutions
, for instance, has infinitely many quaternion solutions 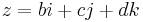 with
with 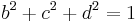 , so that these solutions lie on the two-dimensional surface of a sphere centered on zero in the three-dimensional subspace of quaternions with zero real part. This sphere intersects the complex plane at the two poles
, so that these solutions lie on the two-dimensional surface of a sphere centered on zero in the three-dimensional subspace of quaternions with zero real part. This sphere intersects the complex plane at the two poles  and
and 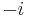 .
.
The fact that quaternion multiplication is not commutative makes the quaternions an often-cited example of a strictly skew field.
Historical impact on physics
In 1984 the European Journal of Physics (5:25–32) published P.R. Girard’s essay The quaternion group and modern physics. It "shows how various physical covariance groups: SO(3), the Lorentz group, the general relativity group, the Clifford algebra SU(2), and the conformal group can be readily related to the quaternion group" in modern algebra. Girard began by discussing group representations and by representing some space groups of crystallography. He proceeded to kinematics of rigid body motion. Next he used complex quaternions (biquaternions) to represent the Lorentz group of special relativity, including the Thomas precession. He cited five authors, beginning with Ludwik Silberstein who use a potential function of one quaternion variable to express Maxwell's equations in a single differential equation. Concerning general relativity, he expressed the Runge–Lenz vector. He mentioned the Clifford biquaternions (split-biquaternions) as an instance of Clifford algebra. Finally, invoking the reciprocal of a biquaternion, Girard described conformal maps on spacetime. Among the fifty references, Girard included Alexander Macfarlane and his Bulletin of the Quaternion Society. In 1999 he showed how Einstein's equations of general relativity could be formulated within a Clifford algebra that is directly linked to quaternions.[11]
A more personal view of quaternions was written by Jim Lambek in 1995. In the Mathematical Intelligencer (17(4):7) he contributed "If Hamilton Had Prevailed: Quaternions in Physics" which recalled the use of biquaternions: "My own interest as a graduate student was raised by the inspiring book by Silberstein". He concluded by stating "I firmly believe that quaternions can supply a shortcut for pure mathematicians who wish to familiarize themselves with certain aspects of theoretical physics."
In 2007, Alexander P. Yefremov and co-workers showed that quaternion space geometry is closely linked to the Yang–Mills field and pointed out connections to the Duffin–Kemmer–Petiau equation and the Klein–Gordon equation.[12]
Sums of four squares
Quaternions are also used in one of the proofs of Lagrange's four-square theorem in number theory, which states that every nonnegative integer is the sum of four integer squares. As well as being an elegant theorem in its own right, Lagrange's four square theorem has useful applications in areas of mathematics outside number theory, such as combinatorial design theory. The quaternion-based proof uses Hurwitz quaternions, a subring of the ring of all quaternions for which there is an analog of the Euclidean algorithm.
Conjugation, the norm, and reciprocal
Conjugation of quaternions is analogous to conjugation of complex numbers and to transposition (also known as reversal) of elements of Clifford algebras. To define it, let q = a +bi +cj + dk be a quaternion. The conjugate of q is the quaternion a − bi − cj − dk. It is denoted by q*, 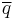 ,[4] qt, or
,[4] qt, or 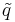 . Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.
. Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.
Unlike the situation in the complex plane, the conjugation of a quaternion can be expressed entirely with multiplication and addition:
Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p*)/2, and the vector part of p is (p − p*)/2.
The square root of the product of a quaternion with its conjugate is called its norm and is denoted ||q||. (Hamilton called this quantity the tensor of q, but this conflicts with modern usage. See tensor.) It has the formula
This is always a non-negative real number, and it is the same as the Euclidean norm on H considered as the vector space R4. Multiplying a quaternion by a real number scales its norm by the absolute value of the number. That is, if α is real, then
This is a special case of the fact that the norm is multiplicative, meaning that
for any two quaternions p and q. Multiplicativity is a consequence of the formula for the conjugate of a product. Alternatively multiplicativity follows directly from the corresponding property of determinants of square matrices and the formula
where i denotes the usual imaginary unit.
This norm makes it possible to define the distance d(p, q) between p and q as the norm of their difference:
This makes H into a metric space. Addition and multiplication are continuous in the metric topology.
A unit quaternion is a quaternion of norm one. Dividing a non-zero quaternion q by its norm produces a unit quaternion Uq called the versor of q:
Every quaternion has a polar decomposition q = ||q|| Uq.
Using conjugation and the norm makes it possible to define the reciprocal of a quaternion. The product of a quaternion with its reciprocal should equal 1, and the considerations above imply that the product of  and
and 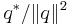 (in either order) is 1. So the reciprocal of q is defined to be
(in either order) is 1. So the reciprocal of q is defined to be
This makes it possible to divide two quaternions p and q in two different ways. That is, their quotient can be either pq−1 or q−1p. The notation 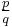 is ambiguous because it does not specify whether q divides on the left or the right.
is ambiguous because it does not specify whether q divides on the left or the right.
Algebraic properties
The set H of all quaternions is a vector space over the real numbers with dimension 4. (In comparison, the real numbers have dimension 1, the complex numbers have dimension 2, and the octonions have dimension 8.) The quaternions have a multiplication that is associative and that distributes over vector addition, but which is not commutative. Therefore the quaternions H are a non-commutative associative algebra over the real numbers. Even though H contains copies of the complex numbers, it is not an associative algebra over the complex numbers.
Because it is possible to divide quaternions, they form a division algebra. This is a structure similar to a field except for the commutativity of multiplication. Finite-dimensional associative division algebras over the real numbers are very rare. The Frobenius theorem states that there are exactly three: R, C, and H. The norm makes the quaternions into a normed algebra, and normed division algebras over the reals are also very rare: Hurwitz's theorem says that there are only four: R, C, H, and O (the octonions). The quaternions are also an example of a composition algebra and of a unital Banach algebra.
Because the product of any two basis vectors is plus or minus another basis vector, the set {±1, ±i, ±j, ±k} forms a group under multiplication. This group is called the quaternion group and is denoted Q8.[13] The real group ring of Q8 is a ring RQ8 which is also an eight-dimensional vector space over R. It has one basis vector for each element of Q8. The quaternions are the quotient ring of RQ8 by the ideal generated by the elements 1 + (−1), i + (−i), j + (−j), and k + (−k). Here the first term in each of the differences is one of the basis elements 1, i, j, and k, and the second term is one of basis elements −1, −i, −j, and −k, not the additive inverses of 1, i, j, and k.
Quaternions and the geometry of R3
Because the vector part of a quaternion is a vector in R3, the geometry of R3 is reflected in the algebraic structure of the quaternions. Many operations on vectors can be defined in terms of quaternions, and this makes it possible to apply quaternion techniques wherever spatial vectors arise. For instance, this is true in electrodynamics and 3D computer graphics.
For the remainder of this section, i, j, and k will denote both imaginary[14] basis vectors of H and a basis for R3. Notice that replacing i by −i, j by −j, and k by −k sends a vector to its additive inverse, so the additive inverse of a vector is the same as its conjugate as a quaternion. For this reason, conjugation is sometimes called the spatial inverse.
Choose two imaginary quaternions p = b1i + c1j + d1k and q = b2i + c2j + d2k. Their dot product is
This is equal to the scalar parts of p*q, qp*, pq*, and q*p. (Note that the vector parts of these four products are different.) It also has the formulas
The cross product of p and q relative to the orientation determined by the ordered basis i, j, and k is
(Recall that the orientation is necessary to determine the sign.) This is equal to the vector part of the product pq (as quaternions), as well as the vector part of −q*p*. It also has the formula
In general, let p and q be quaternions (possibly non-imaginary), and write
where ps and qs are the scalar parts of p and q and 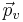 and
and 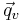 are the vector parts of p and q. Then we have the formula
are the vector parts of p and q. Then we have the formula
This shows that the noncommutativity of quaternion multiplication comes from the multiplication of pure imaginary quaternions. It also shows that two quaternions commute if and only if their vector parts are collinear.
For further elaboration on modeling three-dimensional vectors using quaternions, see quaternions and spatial rotation.
Matrix representations
Just as complex numbers can be represented as matrices, so can quaternions. There are at least two ways of representing quaternions as matrices in such a way that quaternion addition and multiplication correspond to matrix addition and matrix multiplication. One is to use 2×2 complex matrices, and the other is to use 4×4 real matrices. In the terminology of abstract algebra, these are injective homomorphisms from H to the matrix rings M2(C) and M4(R), respectively.
Using 2×2 complex matrices, the quaternion a + bi + cj + dk can be represented as
This representation has the following properties:
- Complex numbers (c = d = 0) correspond to diagonal matrices.
- The norm of a quaternion (the square root of a product with its conjugate, as with complex numbers) is the square root of the determinant of the corresponding matrix.[15]
- The conjugate of a quaternion corresponds to the conjugate transpose of the matrix.
- Restricted to unit quaternions, this representation provides an isomorphism between S3 and SU(2). The latter group is important for describing spin in quantum mechanics; see Pauli matrices.
Using 4×4 real matrices, that same quaternion can be written as
In this representation, the conjugate of a quaternion corresponds to the transpose of the matrix. The fourth power of the norm of a quaternion is the determinant of the corresponding matrix. Complex numbers are block diagonal matrices with two 2×2 blocks.
Quaternions as pairs of complex numbers
Quaternions can be represented as pairs of complex numbers. From this perspective, quaternions are the result of applying the Cayley–Dickson construction to the complex numbers. This is a generalization of the construction of the complex numbers as pairs of real numbers.
Let C2 be a two-dimensional vector space over the complex numbers. Choose a basis consisting of two elements 1 and j. A vector in C2 can be written in terms of the basis elements 1 and j as
If we define j2 = −1 and ij = −ji, then we can multiply two vectors using the distributive law. Writing k in place of the product ij leads to the same rules for multiplication as the usual quaternions. Therefore the above vector of complex numbers corresponds to the quaternion a + bi + cj + dk. If we write the elements of C2 as ordered pairs and quaternions as quadruples, then the correspondence is
Square roots of −1
In the complex numbers, there are just two numbers, i and −i, whose square is −1 . In H there are infinitely many square roots of minus one: the quaternion solution for the square root of −1 is the surface of the unit sphere in 3-space. To see this, let q = a + bi + cj + dk be a quaternion, and assume that its square is −1. In terms of a, b, c, and d, this means
To satisfy the last three equations, either a = 0 or b, c, and d are all 0. The latter is impossible because a is a real number and the first equation would imply that a2 = −1. Therefore a = 0 and b2 + c2 + d2 = 1. In other words, a quaternion squares to −1 if and only if it is a vector (that is, pure imaginary) with norm 1. By definition, the set of all such vectors forms the unit sphere.
Only negative real quaternions have an infinite number of square roots. All others have just two (or one in the case of 0).
The identification of the square roots of minus one in H was given by Hamilton[16] but was frequently omitted in other texts. By 1971 the sphere was included by Sam Perlis in his three page exposition included in Historical Topics in Algebra (page 39) published by the National Council of Teachers of Mathematics. More recently, the sphere of square roots of minus one is described in Ian R. Porteous's book Clifford Algebras and the Classical Groups (Cambridge, 1995) in proposition 8.13 on page 60. Also in Conway (2003) On Quaternions and Octonions we read on page 40: "any imaginary unit may be called i, and perpendicular one j, and their product k", another statement of the sphere.
H as a union of complex planes
Each square root of −1 creates a distinct copy of the complex numbers inside the quaternions. If q2 = −1, then the copy is determined by the function
In the language of abstract algebra, each is an injective ring homomorphism from C to H. The images of the embeddings corresponding to q and -q are identical.
Every non-real quaternion lies in a unique copy of C. Write q as the sum of its scalar part and its vector part:
Decompose the vector part further as the product of its norm and its versor:
(Note that this is not the same as 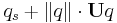 .) The versor of the vector part of q,
.) The versor of the vector part of q, 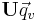 , is a pure imaginary unit quaternion, so its square is −1. Therefore it determines a copy of the complex numbers by the function
, is a pure imaginary unit quaternion, so its square is −1. Therefore it determines a copy of the complex numbers by the function
Under this function, q is the image of the complex number 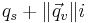 . Thus H is the union of complex planes intersecting in a common real line, where the union is taken over the sphere of square roots of minus one.
. Thus H is the union of complex planes intersecting in a common real line, where the union is taken over the sphere of square roots of minus one.
Commutative subrings
The relationship of quaternions to each other within the complex subplanes of H can also be identified and expressed in terms of commutative subrings. Specifically, since two quaternions p and q commute (p q = q p) only if they lie in the same complex subplane of H, the profile of H as a union of complex planes arises when one seeks to find all commutative subrings of the quaternion ring. This method of commutative subrings is also used to profile the coquaternions and 2 × 2 real matrices.
Functions of a quaternion variable
Like functions of a complex variable, functions of a quaternion variable suggest useful physical models. For example, the original electric and magnetic fields described by Maxwell were functions of a quaternion variable.
Exponential, logarithm, and power
The exponential and logarithm of a quaternion are relatively inexpensive to compute, particularly compared with the cost of those operations for other charts on SO(3) such as rotation matrices, which require computing the matrix exponential and matrix logarithm respectively.
Given a quaternion,
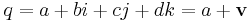 ,
,
the exponential is computed as
and
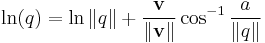 .[17]
.[17]
It follows that the polar decomposition of a quaternion may be written
where the angle  and the unit vector
and the unit vector 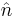 are defined by:
are defined by:
and
Any unit quaternion may be expressed in polar form as 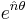 .
.
The power of a quaternion raised to an arbitrary (real) exponent is given by:
Three-dimensional and four-dimensional rotation groups
The term "conjugation", besides the meaning given above, can also mean taking an element a to r a r-1 where r is some non-zero element (quaternion). All elements that are conjugate to a given element (in this sense of the word conjugate) have the same real part and the same norm of the vector part. (Thus the conjugate in the other sense is one of the conjugates in this sense.)
Thus the multiplicative group of non-zero quaternions acts by conjugation on the copy of R³ consisting of quaternions with real part equal to zero. Conjugation by a unit quaternion (a quaternion of absolute value 1) with real part cos(θ) is a rotation by an angle 2θ, the axis of the rotation being the direction of the imaginary part. The advantages of quaternions are:
- Non singular representation (compared with Euler angles for example).
- More compact (and faster) than matrices.
- Pairs of unit quaternions represent a rotation in 4D space (see Rotations in 4-dimensional Euclidean space: Algebra of 4D rotations).
The set of all unit quaternions (versors) forms a 3-dimensional sphere S³ and a group (a Lie group) under multiplication. S³ is the double cover of the group SO(3,R) of real orthogonal 3×3 matrices of determinant 1 since two unit quaternions correspond to every rotation under the above correspondence.
The image of a subgroup of S³ is a point group, and conversely, the preimage of a point group is a subgroup of S³. The preimage of a finite point group is called by the same name, with the prefix binary. For instance, the preimage of the icosahedral group is the binary icosahedral group.
The group S³ is isomorphic to SU(2), the group of complex unitary 2×2 matrices of determinant 1.
Let A be the set of quaternions of the form a + bi + cj + dk where a, b, c, and d are either all integers or all rational numbers with odd numerator and denominator 2. The set A is a ring (in fact a domain) and a lattice and is called the ring of Hurwitz quaternions. There are 24 unit quaternions in this ring, and they are the vertices of a 24-cell regular polytope with Schläfli symbol {3,4,3}.
Generalizations
If F is any field with characteristic different from 2, and a and b are elements of F, one may define a four-dimensional unitary associative algebra over F with basis 1, i, j, and ij, where i2 = a, j2 = b and ij = −ji (so ij2 = −ab). These algebras are called quaternion algebras and are isomorphic to the algebra of 2×2 matrices over F or form division algebras over F, depending on the choice of a and b.
Quaternions as the even part of Cℓ3,0(R)
The usefulness of quaternions for geometrical computations can be generalised to other dimensions, by identifying the quaternions as the even part Cℓ+3,0(R) of the Clifford algebra Cℓ3,0(R). This is an associative multivector algebra built up from fundamental basis elements σ1, σ2, σ3 using the product rules
If these fundamental basis elements are taken to represent vectors in 3D space, then it turns out that the reflection of a vector r in a plane perpendicular to a unit vector w can be written:
Two reflections make a rotation by an angle twice the angle between the two reflection planes, so
corresponds to a rotation of 180° in the plane containing σ1 and σ2. This is very similar to the corresponding quaternion formula,
In fact, the two are identical, if we make the identification
and it is straightforward to confirm that this preserves the Hamilton relations
In this picture, quaternions correspond not to vectors but to bivectors, quantities with magnitude and orientations associated with particular 2D planes rather than 1D directions. The relation to complex numbers becomes clearer, too: in 2D, with two vector directions σ1 and σ2, there is only one bivector basis element σ1σ2, so only one imaginary. But in 3D, with three vector directions, there are three bivector basis elements σ1σ2, σ2σ3, σ3σ1, so three imaginaries.
This reasoning extends further. In the Clifford algebra Cℓ4,0(R), there are six bivector basis elements, since with four different basic vector directions, six different pairs and therefore six different linearly independent planes can be defined. Rotations in such spaces using these generalisations of quaternions, called rotors, can be very useful for applications involving homogeneous coordinates. But it is only in 3D that the number of basis bivectors equals the number of basis vectors, and each bivector can be identified as a pseudovector.
Dorst et al. identify the following advantages for placing quaternions in this wider setting:[18]
- Rotors are natural and non-mysterious in geometric algebra and easily understood as the encoding of a double reflection.
- In geometric algebra, a rotor and the objects it acts on live in the same space. This eliminates the need to change representations and to encode new data structures and methods (which is required when augmenting linear algebra with quaternions).
- A rotor is universally applicable to any element of the algebra, not just vectors and other quaternions, but also lines, planes, circles, spheres, rays, and so on.
- In the conformal model of Euclidean geometry, rotors allow the encoding of rotation, translation and scaling in a single element of the algebra, universally acting on any element. In particular, this means that rotors can represent rotations around an arbitrary axis, whereas quaternions are limited to an axis through the origin.
- Rotor-encoded transformations make interpolation particularly straightforward.
For further detail about the geometrical uses of Clifford algebras, see Geometric algebra.
Brauer group
The quaternions are "essentially" the only (non-trivial) central simple algebra (CSA) over the real numbers, in the sense that every CSA over the reals is Brauer equivalent to either the reals or the quaternions. Explicitly, the Brauer group of the reals consists of two classes, represented by the reals and the quaternions, where the Brauer group is the set of all CSAs, up to equivalence relation of one CSA being a matrix ring over another. By the Artin–Wedderburn theorem (specifically, Wedderburn's part), CSAs are all matrix algebras over a division algebra, and thus the quaternions are the only non-trivial division algebra over the reals.
CSAs – rings over a field, which are simple algebras (have no non-trivial 2-sided ideals, just as with fields) whose center is exactly the field – are a noncommutative analog of extension fields, and are more restrictive than general ring extensions. The fact that the quaternions are the only non-trivial CSA over the reals (up to equivalence) may be compared with the fact that the complex numbers are the only non-trivial field extension of the reals.
Quotes
- "I regard it as an inelegance, or imperfection, in quaternions, or rather in the state to which it has been hitherto unfolded, whenever it becomes or seems to become necessary to have recourse to x, y, z, etc." — William Rowan Hamilton (ed. Quoted in a letter from Tait to Cayley).
- "Time is said to have only one dimension, and space to have three dimensions. […] The mathematical quaternion partakes of both these elements; in technical language it may be said to be "time plus space", or "space plus time": and in this sense it has, or at least involves a reference to, four dimensions. And how the One of Time, of Space the Three, Might in the Chain of Symbols girdled be." — William Rowan Hamilton (Quoted in R.P. Graves, "Life of Sir William Rowan Hamilton").
- "Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way, including Clerk Maxwell." — Lord Kelvin, 1892.
- "Neither matrices nor quaternions and ordinary vectors were banished from these ten [additional] chapters. For, in spite of the uncontested power of the modern Tensor Calculus, those older mathematical languages continue, in my opinion, to offer conspicuous advantages in the restricted field of special relativity. Moreover, in science as well as in every-day life, the mastery of more than one language is also precious, as it broadens our views, is conducive to criticism with regard to, and guards against hypostasy [weak-foundation] of, the matter expressed by words or mathematical symbols." — Ludwik Silberstein, preparing the second edition of his Theory of Relativity in 1924.
- "… quaternions appear to exude an air of nineteenth century decay, as a rather unsuccessful species in the struggle-for-life of mathematical ideas. Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions but, alas, such enthusiasm means little to the harder-headed physical scientist." — Simon L. Altmann, 1986.
- "...the thing about a Quaternion 'is' is that we're obliged to encounter it in more than one guise. As a vector quotient. As a way of plotting complex numbers along three axes instead of two. As a list of instructions for turning one vector into another..... And considered subjectively, as an act of becoming longer or shorter, while at the same time turning, among axes whose unit vector is not the familiar and comforting 'one' but the altogether disquieting square root of minus one. If you were a vector, mademoiselle, you would begin in the 'real' world, change your length, enter an 'imaginary' reference system, rotate up to three different ways, and return to 'reality' a new person. Or vector..." — Thomas Pynchon, Against the Day, 2006.
See also
- 3-sphere
- Associative algebra
- Biquaternion
- Clifford algebra
- Complex number
- Conversion between quaternions and Euler angles
- Division algebra
- Dual quaternion
- Euler Angles
- Exterior algebra
- Geometric algebra
- Hurwitz quaternion
- Hurwitz quaternion order
- Hyperbolic quaternion
- Hypercomplex number
- Octonion
- Quaternion group
- Quaternionic matrix
- Quaternions and spatial rotation
- Simultaneous orthogonal rotations angle
- Rotation operator (vector space)
- Slerp
- SO(4)
- Split-quaternion (Coquaternion)
- Tesseract
Notes
- ^ Hamilton. Hodges and Smith. 1853. p. 60. http://books.google.com/?id=TCwPAAAAIAAJ&printsec=frontcover&dq=quaternion+quotient+lines+tridimensional+space+time#PPA60,M1.
- ^ Hardy 1881 pg. 32. Ginn, Heath, & co.. 1881. http://books.google.com/?id=YNE2AAAAMAAJ&printsec=frontcover&dq=quotient+two+vectors+called+quaternion#PPA32,M1.
- ^ Journal of Theoretics. http://www.journaloftheoretics.com/articles/3-6/qm-pub.pdf.
- ^ a b c See Hazewinkel et. al. (2004), p. 12.
- ^ Conway, John Horton; Smith, Derek Alan (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. p. 9. ISBN 1-56881-134-9. http://books.google.com/books?id=E_HCwwxMbfMC&pg=PA9.
- ^ Robert E. Bradley, Charles Edward Sandifer (2007). Leonhard Euler: life, work and legacy. p. 193. ISBN 0-444-52728-1. http://books.google.com/books?id=75vJL_Y-PvsC&pg=PA193.. They mention Wilhelm Blaschke's claim in 1959 that "the quaternions were first identified by L. Euler in a letter to Goldbach written on May 4, 1748," and they comment that "it makes no sense whatsoever to say that Euler "identified" the quaternions in this letter... this claim is absurd."
- ^ Simon L. Altmann (December 1989). "Hamilton, Rodrigues, and the Quaternion Scandal". Mathematics Magazine 62 (5): 306. http://www.jstor.org/stable/2689481.
- ^ Ken Shoemake (1985). "Animating Rotation with Quaternion Curves". Computer Graphics 19 (3): 245–254. doi:10.1145/325165.325242. http://www.cs.cmu.edu/~kiranb/animation/p245-shoemake.pdf. Presented at SIGGRAPH '85.
Tomb Raider (1996) is often cited as the first mass-market computer game to have used quaternions to achieve smooth three-dimensional rotations. See, for example, Nick Bobick's, "Rotating Objects Using Quaternions", Game Developer magazine, July 1998 - ^ Hamilton, Sir William Rowan (1866). Hamilton Elements of Quaternions article 285. p. 310]. http://books.google.com/?id=fIRAAAAAIAAJ&pg=PA117&dq=quaternion#PPA310,M1.
- ^ Hardy Elements of quaternions. library.cornell.edu. p. 65. http://dlxs2.library.cornell.edu/cgi/t/text/pageviewer-idx?c=math;cc=math;q1=right%20quaternion;rgn=full%20text;idno=05140001;didno=05140001;view=image;seq=81.
- ^ Einstein's equations and Clifford algebra, Advances in Applied Clifford Algebras 9 No. 2, 225-230 (1999)
- ^ A. Yefremov, F. Smarandache, V. Christianto: Yang-Mills field from quaternion space geometry, and its Klein-Gordon representation, Progress in Physics, vol. 3, July 2007, pp. 42–50. Also in Florentin Smarandache (ed.): Hadron Models and Related New Energy Issues, InfoLearnQuest, 2007, ISBN 978-1-59973-042-4, p. 208–219
- ^ "quaternion group". Wolframalpha.com. http://www.wolframalpha.com/input/?i=quaternion+group.
- ^ Vector Analysis. Gibbs-Wilson. 1901. p. 428. http://books.google.com/?id=RC8PAAAAIAAJ&printsec=frontcover&dq=right+tensor+dyadic#PPA428,M1.
- ^ Wolframalpha.com
- ^ Hamilton (1899). Elements of Quaternions (2nd ed.). p. 244. ISBN 1108001718.
- ^ Lce.hut.fi
- ^ Quaternions and Geometric Algebra. Accessed 2008-09-12. See also: Leo Dorst, Daniel Fontijne, Stephen Mann, (2007), Geometric Algebra For Computer Science, Morgan Kaufmann. ISBN 0-12-369465-5
External articles and resources
Books and publications
- Hamilton, William Rowan. On quaternions, or on a new system of imaginaries in algebra. Philosophical Magazine. Vol. 25, n 3. p. 489–495. 1844.
- Hamilton, William Rowan (1853), "Lectures on Quaternions". Royal Irish Academy.
- Hamilton (1866) Elements of Quaternions University of Dublin Press. Edited by William Edwin Hamilton, son of the deceased author.
- Hamilton (1899) Elements of Quaternions volume I, (1901) volume II. Edited by Charles Jasper Joly; published by Longmans, Green & Co..
- Tait, Peter Guthrie (1873), "An elementary treatise on quaternions". 2d ed., Cambridge, [Eng.] : The University Press.
- Michiel Hazewinkel, Nadiya Gubareni, Nadezhda Mikhaĭlovna Gubareni, Vladimir V. Kirichenko. Algebras, rings and modules. Volume 1. 2004. Springer, 2004. ISBN 1-4020-2690-0
- Maxwell, James Clerk (1873), "A Treatise on Electricity and Magnetism". Clarendon Press, Oxford.
- Tait, Peter Guthrie (1886), "Quaternion". M.A. Sec. R.S.E. Encyclopaedia Britannica, Ninth Edition, 1886, Vol. XX, pp. 160–164. (bzipped PostScript file)
- Joly, Charles Jasper (1905), "A manual of quaternions". London, Macmillan and co., limited; New York, The Macmillan company. LCCN 05036137 //r84
- Macfarlane, Alexander (1906), "Vector analysis and quaternions", 4th ed. 1st thousand. New York, J. Wiley & Sons; [etc., etc.]. LCCN es 16000048
- 1911 encyclopedia: "Quaternions".
- Finkelstein, David, Josef M. Jauch, Samuel Schiminovich, and David Speiser (1962), "Foundations of quaternion quantum mechanics". J. Mathematical Phys. 3, pp. 207–220, MathSciNet.
- Du Val, Patrick (1964), "Homographies, quaternions, and rotations". Oxford, Clarendon Press (Oxford mathematical monographs). LCCN 64056979 //r81
- Crowe, Michael J. (1967), A History of Vector Analysis: The Evolution of the Idea of a Vectorial System, University of Notre Dame Press. Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley, Gibbs, Heaviside).
- Altmann, Simon L. (1986), "Rotations, quaternions, and double groups". Oxford [Oxfordshire] : Clarendon Press ; New York : Oxford University Press. LCCN 85013615 ISBN 0-19-855372-2
- Altmann, Simon L. (1989), "Hamilton, Rodrigues, and the Quaternion Scandal". Mathematics Magazine. Vol. 62, No. 5. p. 291–308, Dec. 1989.
- Adler, Stephen L. (1995), "Quaternionic quantum mechanics and quantum fields". New York : Oxford University Press. International series of monographs on physics (Oxford, England) 88. LCCN 94006306 ISBN 0-19-506643-X
- Trifonov, Vladimir (1995), "A Linear Solution of the Four-Dimensionality Problem", Europhysics Letters, 32 (8) 621–626, DOI: 10.1209/0295-5075/32/8/001
- Ward, J. P. (1997), "Quaternions and Cayley Numbers: Algebra and Applications", Kluwer Academic Publishers. ISBN 0-7923-4513-4
- Kantor, I. L. and Solodnikov, A. S. (1989), "Hypercomplex numbers, an elementary introduction to algebras", Springer-Verlag, New York, ISBN 0-387-96980-2
- Gürlebeck, Klaus and Sprössig, Wolfgang (1997), "Quaternionic and Clifford calculus for physicists and engineers". Chichester ; New York : Wiley (Mathematical methods in practice; v. 1). LCCN 98169958 ISBN 0-471-96200-7
- Kuipers, Jack (2002), "Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality" (reprint edition), Princeton University Press. ISBN 0-691-10298-8
- Conway, John Horton, and Smith, Derek A. (2003), "On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry", A. K. Peters, Ltd. ISBN 1-56881-134-9 (review).
- Kravchenko, Vladislav (2003), "Applied Quaternionic Analysis", Heldermann Verlag ISBN 3-88538-228-8.
- Hanson, Andrew J. (2006), "Visualizing Quaternions", Elsevier: Morgan Kaufmann; San Francisco. ISBN 0-12-088400-3
- Trifonov, Vladimir</ref> (2007), "Natural Geometry of Nonzero Quaternions", International Journal of Theoretical Physics, 46 (2) 251–257, DOI: 10.1007/s10773-006-9234-9
- Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical Society, Chapter 1: "The Skew Field of Quaternions" (23 pages) ISBN 978-0-8218-4495-3.
- Vince, John A. (2008), Geometric Algebra for Computer Graphics, Springer, ISBN 978-1-84628-996-5.
- For molecules that can be regarded as classical rigid bodies molecular dynamics computer simulation employs quaternions. They were first introduced for this purpose by D.J. Evans, (1977), "On the Representation of Orientation Space", Mol. Phys., vol 34, p 317.
Links and monographs
- Matrix and Quaternion FAQ v1.21 Frequently Asked Questions
- "Geometric Tools documentation" (frame; body) includes several papers focusing on computer graphics applications of quaternions. Covers useful techniques such as spherical linear interpolation.
- Patrick-Gilles Maillot Provides free Fortran and C source code for manipulating quaternions and rotations / position in space. Also includes mathematical background on quaternions.
- "Geometric Tools source code" (frame; body) includes free C++ source code for a complete quaternion class suitable for computer graphics work, under a very liberal license.
- Doug Sweetser, Doing Physics with Quaternions
- Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
- The Physical Heritage of Sir W. R. Hamilton (PDF)
- D. R. Wilkins, Hamilton’s Research on Quaternions
- Quaternion Julia Fractals 3D Raytraced Quaternion Julia Fractals by David J. Grossman
- Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
- John H. Mathews, Bibliography for Quaternions.
- Quaternion powers on GameDev.net
- Andrew Hanson, Visualizing Quaternions home page.
- Representing Attitude with Euler Angles and Quaternions: A Reference, Technical report and Matlab toolbox summarizing all common attitude representations, with detailed equations and discussion on features of various methods.
- Charles F. F. Karney, Quaternions in molecular modeling, J. Mol. Graph. Mod. 25(5), 595–604 (Jan. 2007); DOI: 10.1016/j.jmgm.2006.04.002; E-print arxiv:0506177.
- Johan E. Mebius, A matrix-based proof of the quaternion representation theorem for four-dimensional rotations., arXiv General Mathematics 2005.
- Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- NUI Maynooth Department of Mathematics, Hamilton Walk.
- OpenGL:Tutorials:Using Quaternions to represent rotation
- David Erickson, Defence Research and Development Canada (DRDC), Complete derivation of rotation matrix from unitary quaternion representation in DRDC TR 2005-228 paper. Drdc-rddc.gc.ca
- Alberto Martinez, University of Texas Department of History, "Negative Math, How Mathematical Rules Can Be Positively Bent",Utexas.edu
- D. Stahlke, Quaternions in Classical Mechanics Stahlke.org (PDF)
- Morier-Genoud, Sophie, and Valentin Ovsienko. "Well, Papa, can you multiply triplets?", arxiv.org describes how the quaternions can be made into a skew-commutative algebra graded by Z/2×Z/2×Z/2.
- Curious Quaternions by Helen Joyce hosted by John Baez.
- Luis Ibanez "Tutorial on Quaternions" Part I Part II (PDF)
Software
- Quaternion Calculator [javascript], bluetulip.org
- Quaternion Calculator [Java], theworld.com
- Quaternion Toolbox for Matlab, qtfm.sourceforge.net
- Boost library support for Quaternions in C++, boost.org
- Mathematics of flight simulation >Turbo-PASCAL software for quaternions, Euler angles and Extended Euler angles, xs4all.nl
|
|||||||||||
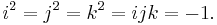
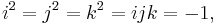
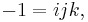
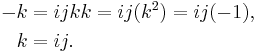
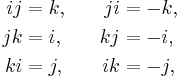
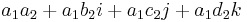
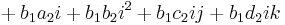
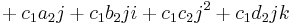
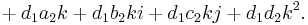
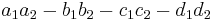
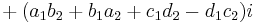
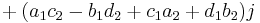
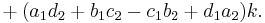
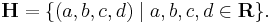
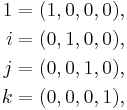
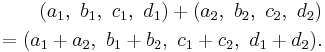
![\begin{align}
& (a_1,\ b_1,\ c_1,\ d_1)(a_2,\ b_2,\ c_2,\ d_2) \\[8pt]
& = (a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2, \\
& {} \qquad a_1b_2 %2B b_1a_2 %2B c_1d_2 - d_1c_2, \\
& {} \qquad a_1c_2 - b_1d_2 %2B c_1a_2 %2B d_1b_2, \\
& {} \qquad a_1d_2 %2B b_1c_2 - c_1b_2 %2B d_1a_2).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/061966d3ddbdcaa74039083dd06df697.png)
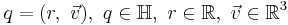
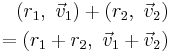
![\begin{array}{c}
(r_1,\ \vec{v}_1) (r_2,\ \vec{v}_2) \\[8pt]
\begin{align}
& = (r_1 r_2 - \vec{v}_1\cdot\vec{v}_2,\\
& {} \qquad r_1\vec{v}_2%2Br_2\vec{v}_1 %2B \vec{v}_1\times\vec{v}_2)
\end{align}
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/b8f3c29bc2278e4545527fe1277332b0.png)
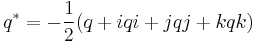
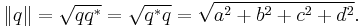
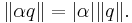
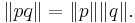
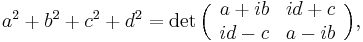
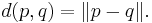
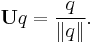
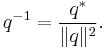
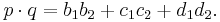
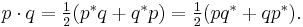
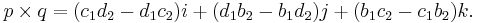
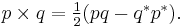
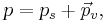
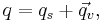
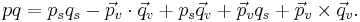
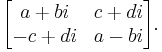
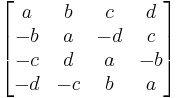

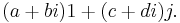
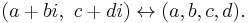
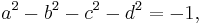
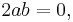
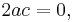
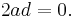
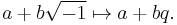
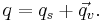
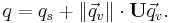
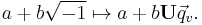
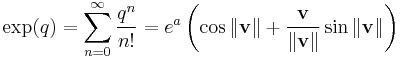
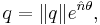
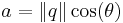
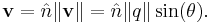
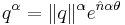
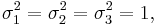
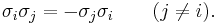
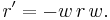
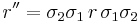
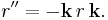
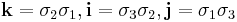
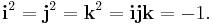
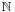 )
)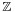 )
) )
) )
) )
) )
)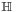 )
) )
)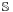 )
)