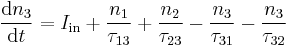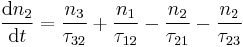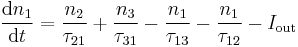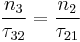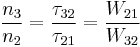Quantum cascade laser
Quantum cascade lasers (QCLs) are semiconductor lasers that emit in the mid- to far-infrared portion of the electromagnetic spectrum and were first demonstrated by Jerome Faist, Federico Capasso, Deborah Sivco, Carlo Sirtori, Albert Hutchinson, and Alfred Cho at Bell Laboratories in 1994.[1]
Unlike typical interband semiconductor lasers that emit electromagnetic radiation through the recombination of electron–hole pairs across the material band gap, QCLs are unipolar and laser emission is achieved through the use of intersubband transitions in a repeated stack of semiconductor multiple quantum well heterostructures, an idea first proposed in the paper "Possibility of amplification of electromagnetic waves in a semiconductor with a superlattice" by R.F. Kazarinov and R.A. Suris in 1971.[2]
Contents |
Intersubband vs. interband transitions
Within a bulk semiconductor crystal, electrons may occupy states in one of two continuous energy bands - the valence band, which is heavily populated with low energy electrons and the conduction band, which is sparsely populated with high energy electrons. The two energy bands are separated by an energy band gap in which there are no permitted states available for electrons to occupy. Conventional semiconductor laser diodes generate light by a single photon being emitted when a high energy electron in the conduction band recombines with a hole in the valence band. The energy of the photon and hence the emission wavelength of laser diodes is therefore determined by the band gap of the material system used.
A QCL however does not use bulk semiconductor materials in its optically active region. Instead it comprises a periodic series of thin layers of varying material composition forming a superlattice. The superlattice introduces a varying electric potential across the length of the device, meaning that there is a varying probability of electrons occupying different positions over the length of the device. This is referred to as one-dimensional multiple quantum well confinement and leads to the splitting of the band of permitted energies into a number of discrete electronic subbands. By suitable design of the layer thicknesses it is possible to engineer a population inversion between two subbands in the system which is required in order to achieve laser emission. Since the position of the energy levels in the system is primarily determined by the layer thicknesses and not the material, it is possible to tune the emission wavelength of QCLs over a wide range in the same material system.
Additionally, in semiconductor laser diodes, electrons and holes are annihilated after recombining across the band gap and can play no further part in photon generation. However in a unipolar QCL, once an electron has undergone an intersubband transition and emitted a photon in one period of the superlattice, it can tunnel into the next period of the structure where another photon can be emitted. This process of a single electron causing the emission of multiple photons as it traverses through the QCL structure gives rise to the name cascade and makes a quantum efficiency of greater than unity possible which leads to higher output powers than semiconductor laser diodes.
Operating principles
Rate equations
QCLs are typically based upon a three-level system. Assuming the formation of the wavefunctions is a fast process compared to the scattering between states, the time independent solutions to the Schrödinger equation may be applied and the system can be modelled using rate equations. Each subband contains a number of electrons 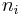 (where
(where  is the subband index) which scatter between levels with a lifetime
is the subband index) which scatter between levels with a lifetime 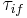 (reciprocal of the average intersubband scattering rate
(reciprocal of the average intersubband scattering rate 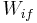 ), where
), where  and
and  are the initial and final subband indices. Assuming that no other subbands are populated, the rate equations for the three level lasers are given by:
are the initial and final subband indices. Assuming that no other subbands are populated, the rate equations for the three level lasers are given by:
In the steady state, the time derivatives are equal to zero and 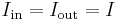 . The general rate equation for electrons in subband i of an N level system is therefore:
. The general rate equation for electrons in subband i of an N level system is therefore:
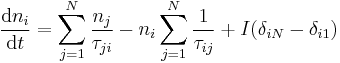 ,
,
Under the assumption that absorption processes can be ignored, (i.e. 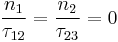 , valid at low temperatures) the middle rate equation gives
, valid at low temperatures) the middle rate equation gives
Therefore if 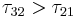 (i.e.
(i.e. 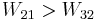 ) then
) then 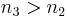 and a population inversion will exist. The population ratio is defined as
and a population inversion will exist. The population ratio is defined as
If all N steady-state rate equations are summed, the right hand side becomes zero, meaning that the system is underdetermined, and it is possible only to find the relative population of each subband. If the total sheet density of carriers 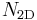 in the system is also known, then the absolute population of carriers in each subband may be determined using:
in the system is also known, then the absolute population of carriers in each subband may be determined using:
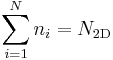 .
.
As an approximation, it can be assumed that all the carriers in the system are supplied by doping. If the dopant species has a negligible ionisation energy then 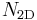 is approximately equal to the doping density.
is approximately equal to the doping density.
Active region designs
The scattering rates are tailored by suitable design of the layer thicknesses in the superlattice which determine the electron wave functions of the subbands. The scattering rate between two subbands is heavily dependent upon the overlap of the wave functions and energy spacing between the subbands. The figure shows the wave functions in a three quantum well (3QW) QCL active region and injector.
In order to decrease 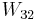 , the overlap of the upper and lower laser levels is reduced. This is often achieved through designing the layer thicknesses such that the upper laser level is mostly localised in the left-hand well of the 3QW active region, while the lower laser level wave function is made to mostly reside in the central and right-hand wells. This is known as a diagonal transition. A vertical transition is one in which the upper laser level is localised in mainly the central and right-hand wells. This increases the overlap and hence
, the overlap of the upper and lower laser levels is reduced. This is often achieved through designing the layer thicknesses such that the upper laser level is mostly localised in the left-hand well of the 3QW active region, while the lower laser level wave function is made to mostly reside in the central and right-hand wells. This is known as a diagonal transition. A vertical transition is one in which the upper laser level is localised in mainly the central and right-hand wells. This increases the overlap and hence 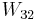 which reduces the population inversion, but it increases the strength of the radiative transition and therefore the gain.
which reduces the population inversion, but it increases the strength of the radiative transition and therefore the gain.
In order to increase 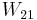 , the lower laser level and the ground level wave functions are designed such that they have a good overlap and to increase
, the lower laser level and the ground level wave functions are designed such that they have a good overlap and to increase 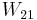 further, the energy spacing between the subbands is designed such that it is equal to the longitudinal optical (LO) phonon energy (~36 meV in GaAs) so that resonant LO phonon-electron scattering can quickly depopulate the lower laser level.
further, the energy spacing between the subbands is designed such that it is equal to the longitudinal optical (LO) phonon energy (~36 meV in GaAs) so that resonant LO phonon-electron scattering can quickly depopulate the lower laser level.
Material systems
The first QCL was fabricated in the InGaAs/InAlAs material system lattice-matched to an InP substrate.[1] This particular material system has a conduction band offset (quantum well depth) of 520 meV. These InP-based devices have reached very high levels of performance across the mid-infrared spectral range, achieving high power, above room-temperature, continuous wave emission.[3]
In 1998 GaAs/AlGaAs QCLs were demonstrated by Sirtori et al. proving that the QC concept is not restricted to one material system. This material system has a varying quantum well depth depending on the aluminium fraction in the barriers. Although GaAs-based QCLs have not matched the performance levels of InP-based QCLs in the mid-infrared, they have proven to be very successful in the terahertz region of the spectrum.
The short wavelength limit of QCLs is determined by the depth of the quantum well and recently QCLs have been developed in material systems with very deep quantum wells in order to achieve short wavelength emission. The InGaAs/AlAsSb material system has quantum wells 1.6 eV deep and has been used to fabricate QCLs emitting at 3 μm. InAs/AlSb QCLs have quantum wells 2.1 eV deep and electroluminescence at wavelengths as short as 2.5 μm has been observed.
QCLs may also allow laser operation in materials traditionally considered to have poor optical properties. Indirect bandgap materials such as silicon have minimum electron and hole energies at different momentum values. For interband optical transitions, carriers change momentum through a slow, intermediate scattering process, dramatically reducing the optical emission intensity. Intersubband optical transitions however, are independent of the relative momentum of conduction band and valence band minima and theoretical proposals for Si/SiGe quantum cascade emitters have been made.[4]
Emission wavelengths
QCLs currently cover the wavelength range from 2.75–250 μm (and extends to 355 μm with the application of a magnetic field).
Optical waveguides
The first step in processing quantum cascade gain material to make a useful light-emitting device is to confine the gain medium in an optical waveguide. This makes it possible to direct the emitted light into a collimated beam, and allows a laser resonator to be built such that light can be coupled back into the gain medium.
Two types of optical waveguides are in common use. A ridge waveguide is created by etching parallel trenches in the quantum cascade gain material to create an isolated stripe of QC material, typically ~10 um wide, and several mm long. A dielectric material is typically deposited in the trenches to guide injected current into the ridge, then the entire ridge is typically coated with gold to provide electrical contact and to help remove heat from the ridge when it is producing light. Light is emitted from the cleaved ends of the waveguide, with an active area that is typically only a few micrometers in dimension.
The second waveguide type is a buried heterostructure. Here, the QC material is also etched to produce an isolated ridge. Now, however, new semiconductor material is grown over the ridge. The change in index of refraction between the QC material and the overgrown material is sufficient to create a waveguide. Dielectric material is also deposited on the overgrown material around QC ridge to guide the injected current into the QC gain medium. Buried heterostructure waveguides are efficient at removing heat from the QC active area when light is being produced.
Laser types
Although the quantum cascade gain medium can be used to produce incoherent light in a superluminescent configuration,[5] it is most commonly used in combination with an optical cavity to form a laser.
Fabry–Pérot lasers
This is the simplest of the quantum cascade lasers. An optical waveguide is first fabricated out of the quantum cascade material to form the gain medium. The ends of the crystalline semiconductor device are then cleaved to form two parallel mirrors on either end of the waveguide, thus forming a Fabry–Pérot resonator. The residual reflectivity on the cleaved facets from the semiconductor-to-air interface is sufficient to create a resonator. Fabry–Pérot quantum cascade lasers are capable of producing high powers,[6] but are typically multi-mode at higher operating currents. The wavelength can be changed chiefly by changing the temperature of the QC device.
Distributed feedback lasers
A distributed feedback (DFB) quantum cascade laser[7] is similar to a Fabry–Pérot laser, except for a distributed Bragg reflector (DBR) built on top of the waveguide to prevent it from emitting at other than the desired wavelength. This forces single mode operation of the laser, even at higher operating currents. DFB lasers can be tuned chiefly by changing the temperature, although an interesting variant on tuning can be obtained by pulsing a DFB laser. In this mode, the wavelength of the laser is rapidly “chirped” during the course of the pulse, allowing rapid scanning of a spectral region.[8]
External cavity lasers
In an external cavity (EC) quantum cascade laser, the quantum cascade device serves as the laser gain medium. One, or both, of the waveguide facets have an anti-reflection coating that defeats the optical cavity action of the cleaved facets. Mirrors are then arranged in a configuration external to the QC device to create the optical cavity.
If a frequency-selective element is included in the external cavity, it is possible to reduce the laser emission to a single wavelength, and even tune the radiation. For example, diffraction gratings have been used to create[9] a tunable laser that can tune over 15% of its center wavelength.
Growth
The alternating layers of the two different semiconductors which form the quantum heterostructure may be grown on to a substrate using a variety of methods such as molecular beam epitaxy (MBE) , metalorganic vapour phase epitaxy (MOVPE), or metalorganic chemical vapor deposition (MOCVD).
Applications
Distributed feedback (DFB) quantum cascade lasers were first commercialized in 2004,[10] and broadly-tunable external cavity quantum cascade lasers first commercialized in 2006.[11] The high optical power output, tuning range and room temperature operation make QCLs useful for spectroscopic applications such as remote sensing of environmental gases and pollutants in the atmosphere[12] and homeland security. They may eventually be used for vehicular cruise control in conditions of poor visibility, collision avoidance radar, industrial process control, and medical diagnostics such as breath analyzers. QCLs are also used to study plasma chemistry.
Their large dynamic range, excellent sensitivity, and failsafe operation combined with the solid-state reliability should easily overcome many of the technological hurdles that impede existing technology in these markets. When used in multiple-laser systems, intrapulse QCL spectroscopy offers broadband spectral coverage that can potentially be used to identify and quantify complex heavy molecules such as those in toxic chemicals, explosives, and drugs.[13]
Unguided QCL emission in the 3–5 μm atmospheric window could be used as a cheaper alternative to optical fibres for high-speed Internet access in built up areas.
References
- ^ a b Faist, Jerome; Federico Capasso, Deborah L. Sivco, Carlo Sirtori, Albert L. Hutchinson, and Alfred Y. Cho (April 1994). "Quantum Cascade Laser" (abstract). Science 264 (5158): 553–556. Bibcode 1994Sci...264..553F. doi:10.1126/science.264.5158.553. PMID 17732739. http://www.sciencemag.org/cgi/content/abstract/264/5158/553. Retrieved 2007-02-18.
- ^ Kazarinov, R.F; Suris, R.A. (April 1971). "Possibility of amplification of electromagnetic waves in a semiconductor with a superlattice". Fizika i Tekhnika Poluprovodnikov 5 (4): 797–800.
- ^ Razeghi, Manijeh (2009). "High-Performance InP-Based Mid-IR Quantum Cascade Lasers" (abstract). IEEE Journal of Selected Topics in Quantum Electronics 15 (3): 941–951. doi:10.1109/JSTQE.2008.2006764. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=5069088. Retrieved 2011-07-13.
- ^ Paul, Douglas J (2004). "Si/SiGe heterostructures: from material and physics to devices and circuits" (abstract). Semicond. Sci. Technol. 19 (10): R75–R108. Bibcode 2004SeScT..19R..75P. doi:10.1088/0268-1242/19/10/R02. http://www.iop.org/EJ/abstract/0268-1242/19/10/R02. Retrieved 2007-02-18.
- ^ Zibik, E. A.; W. H. Ng, D. G. Revin, L. R. Wilson, J. W. Cockburn, K. M. Groom, and M. Hopkinson (March 2006). "Broadband 6 µm < λ < 8 µm superluminescent quantum cascade light-emitting diodes". Appl. Phys. Lett. 88 (12): 121109. Bibcode 2006ApPhL..88l1109Z. doi:10.1063/1.2188371.
- ^ Slivken, S.; A. Evans, J. David, and M. Razeghi (December 2002). "High-average-power, high-duty-cycle (λ ~ 6 µm) quantum cascade lasers". Applied Physics Letters 81 (23): 4321–4323. Bibcode 2002ApPhL..81.4321S. doi:10.1063/1.1526462.
- ^ Faist, Jérome; Claire Gmachl, Frederico Capasso, Carlo Sirtori, Deborah L. Silvco, James N. Baillargeon, and Alfred Y. Cho (May 1997). "Distributed feedback quantum cascade lasers". Applied Physics Letters 70 (20): 2670. Bibcode 1997ApPhL..70.2670F. doi:10.1063/1.119208.
- ^ "Quantum-cascade lasers smell success". Laser Focus World. PennWell Publications. 2005-03-01. http://www.laserfocusworld.com/display_article/224013/12/none/none/OptWr/Quantum-cascade-lasers-smell-success. Retrieved 2008-03-26.
- ^ Maulini, Richard; Mattias Beck, Jérome Faist, and Emilio Gini (March 2004). "Broadband tuning of external cavity bound-to-continuum quantum-cascade lasers". Applied Physics Letters 84 (10): 1659. Bibcode 2004ApPhL..84.1659M. doi:10.1063/1.1667609.
- ^ "Alpes offers CW and pulsed quantum cascade lasers". Laser Focus World. PennWell Publications. 2004-04-19. http://www.laserfocusworld.com/display_article/202916/12/ARCHI/none/PRODH/Alpes-offers-CW-and-pulsed-quantum-cascade-lasers. Retrieved 2007-12-01.
- ^ "Tunable QC laser opens up mid-IR sensing applications". Laser Focus World. PennWell Publications. 2006-07-01. http://www.laserfocusworld.com/display_article/259939/12/none/none/OptWr/Tunable-QC-laser-opens-up-mid-IR-sensing-applications. Retrieved 2008-03-26.
- ^ Normand, Erwan; Howieson, Iain; McCulloch, Michael T. (April 2007). "Quantum-cascade lasers enable gas-sensing technology". Laser Focus World 43 (4): 90–92. ISSN 1043-8092. http://www.laserfocusworld.com/display_article/289410/12/none/none/Feat/QUANTUM-CASCADE-LASERS:-Quantum-cascade-lasers-enable-gas-sensing-technolog. Retrieved 2008-01-25.
- ^ Howieson, Iain; Normand, Erwan; McCulloch, Michael T. (2005-03-01). "Quantum-cascade lasers smell success". Laser Focus World 41 (3): S3–+. ISSN 0740-2511. http://www.laserfocusworld.com/display_article/224013/12/ARCHI/none/OptWr/Quantum-cascade-lasers-smell-success. Retrieved 2008-01-25.