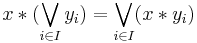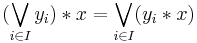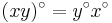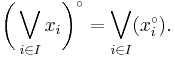Quantale

In mathematics, quantales are certain partially ordered algebraic structures that generalize locales (point free topologies) as well as various multiplicative lattices of ideals from ring theory and functional analysis (C*-algebras, von Neumann algebras). Quantales are sometimes referred to as complete residuated semigroups.

A quantale is a complete lattice Q with an associative binary operation ∗ : Q × Q → Q, called its multiplication, satisfying

x*(\bigvee_{i\in I}{y_i})=\bigvee_{i\in I}(x*y_i)

and

(\bigvee_{i\in I}{y_i})*{x}=\bigvee_{i\in I}(y_i*x)

for all x, yi in Q, i in I (here I is any index set).

The quantale is unital if it is has an identity element e for its multiplication:

x ∗ e = x = e ∗ x

for all x in Q. In this case, the quantale is naturally a monoid with respect to its multiplication ∗.

A unital quantale may be defined equivalently as a monoid in the category Sup of complete join semi-lattices.

A unital quantale is an idempotent semiring, or dioid, under join and multiplication.

A unital quantale in which the identity is the top element of the underlying lattice, is said to be strictly two-sided (or simply integral).

A commutative quantale is a quantale whose multiplication is commutative. A frame, with its multiplication given by the meet operation, is a typical example of a strictly two-sided commutative quantale. Another simple example is provided by the unit interval together with its usual multiplication.

An idempotent quantale is a quantale whose multiplication is idempotent. A frame is the same as an idempotent strictly two-sided quantale.

An involutive quantale is a quantale with an involution:

(xy)^\circ = y^\circ x^\circ

that preserves joins:

\biggl(\bigvee_{i\in I}{x_i}\biggr)^\circ =\bigvee_{i\in I}(x_i^\circ).

References