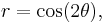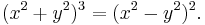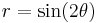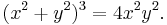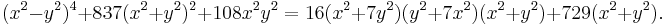Quadrifolium

This article is about a geometric shape. For the article about the plant, please see Four-leaf clover

The quadrifolium (also known as four-leaved clover^[1]) is a type of rose curve with n=2. It has polar equation:

$r = \cos(2\theta), \,$

with corresponding algebraic equation

$(x^2%2By^2)^3 = (x^2-y^2)^2. \,$

Rotated by 45°, this becomes

$r = \sin(2\theta) \,$

with corresponding algebraic equation

$(x^2%2By^2)^3 = 4x^2y^2. \,$

In either form, it is a plane algebraic curve of genus zero.

The dual curve to the quadrifolium is

$(x^2-y^2)^4 %2B 837(x^2%2By^2)^2 %2B 108x^2y^2 = 16(x^2%2B7y^2)(y^2%2B7x^2)(x^2%2By^2)%2B729(x^2%2By^2). \,$

The area inside the curve is 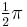$\tfrac 12 \pi$ , which is exactly half of the area of the circumcircle of the quadrifolium. The length of the curve is ca. 9.6884.^[2]

Notes

^ C G Gibson, Elementary Geometry of Algebraic Curves, An Undergraduate Introduction, Cambridge University Press, Cambridge, 2001, ISBN 978-0521-646413. Pages 92 and 93
^ http://mathworld.wolfram.com/Quadrifolium.html

References

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 175. ISBN 0-486-60288-5.

External links

Interactive example with JSXGraph