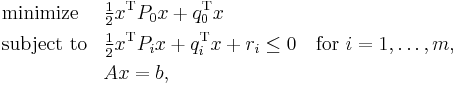Quadratically constrained quadratic program

In mathematics, a quadratically constrained quadratic program (QCQP) is an optimization problem in which both the objective function and the constraints are quadratic functions. It has the form

\begin{align} & \text{minimize} && \tfrac12 x^\mathrm{T} P_0 x %2B q_0^\mathrm{T} x \\ & \text{subject to} && \tfrac12 x^\mathrm{T} P_i x %2B q_i^\mathrm{T} x %2B r_i \leq 0 \quad \text{for } i = 1,\dots,m , \\ &&& Ax = b, \end{align}

where P0, … Pm are n-by-n matrices and x ∈ Rn is the optimization variable.

If P0, … Pm are all positive semidefinite, then the problem is convex. If these matrices are neither positive or negative semidefinite, the problem is non-convex. If these are all zero, then the constraints are in fact linear and the problem is a quadratic program.

Contents

Hardness

Solving the general case is an NP-hard problem. To see this, note that the two constraints x1(x1 − 1) ≤ 0 and x1(x1 − 1) ≥ 0 are equivalent to the constraint x1(x1 − 1) = 0, which is in turn equivalent to the constraint x1 ∈ {0, 1}. Hence, any 0–1 integer program (in which all variables have to be either 0 or 1) can be formulated as a quadratically constrained quadratic program. Since 0–1 integer programming is NP-hard in general, QCQP is also NP-hard.

Relaxation

There are two main relaxations of QCQP: using semidefinite programming (SDP), and using the reformulation-linearization technique (RLT).

Semidefinite programming

When P0, … Pm are all positive-definite matrices, the problem is convex and can be readily solved using interior point methods, as done with semidefinite programming.

Example

Max Cut is a problem in graph theory, which is NP-hard. Given a graph, the problem is to divide the vertices in two sets, so that as many edges as possible go from one set to the other. Max Cut can be formulated as a QCQP, and SDP relaxation of the dual provides good lower bounds.

References