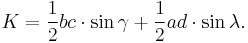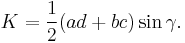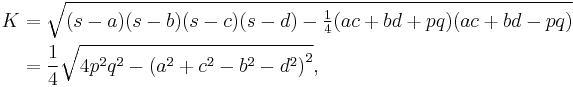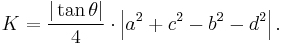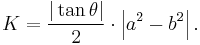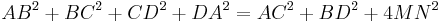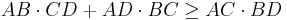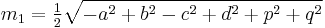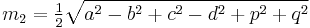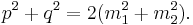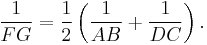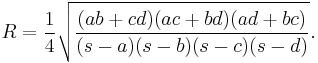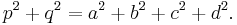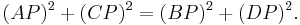Quadrilateral
| Quadrilateral | |
|---|---|
Six different types of quadrilaterals |
|
| Edges and vertices | 4 |
| Schläfli symbol | {4} (for square) |
| Area | various methods; see below |
| Internal angle (degrees) | 90° (for square) |
In Euclidean plane geometry, a quadrilateral is a polygon with four sides (or edges) and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon (5-sided), hexagon (6-sided) and so on. The word quadrilateral is made of the words quad (meaning "four") and lateral (meaning "of sides").
The origin of the word quadrilateral is from the two Latin words "quadri", a variant of four, and "latus" meaning side.
Quadrilaterals are simple (not self-intersecting) or complex (self-intersecting), also called crossed. Simple quadrilaterals are either convex or concave.
The interior angles of a simple quadrilateral add up to 360 degrees of arc. This is a special case of the n-gon interior angle sum formula (n - 2)×180°. In a crossed quadrilateral, the interior angles on either side of the crossing add up to 720°.[1]
All convex quadrilaterals tile the plane by repeated rotation around the midpoints of their edges.
Convex quadrilaterals - parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides. Equivalent conditions are that opposite sides are of equal length; that opposite angles are equal; or that the diagonals bisect each other. Parallelograms also include the square, rectangle, rhombus and rhomboid.
- Rhombus or rhomb: all four sides are of equal length. Equivalent conditions are that opposite sides are parallel and opposite angles are equal, or that the diagonals perpendicularly bisect each other. An informal description is "a pushed-over square" (including a square).
- Rhomboid: a parallelogram in which adjacent sides are of unequal lengths and angles are oblique (not right angles). Informally: "a pushed-over rectangle with no right angles."
- Rectangle: all four angles are right angles. An equivalent condition is that the diagonals bisect each other and are equal in length. Informally: "a box or oblong" (including a square).
- Square (regular quadrilateral): all four sides are of equal length (equilateral), and all four angles are right angles. An equivalent condition is that opposite sides are parallel (a square is a parallelogram), that the diagonals perpendicularly bisect each other, and are of equal length. A quadrilateral is a square if and only if it is both a rhombus and a rectangle (four equal sides and four equal angles).
- Oblong: a term sometimes used to denote a rectangle which has unequal adjacent sides (i.e. a rectangle that is not a square).
Convex quadrilaterals - other
- Kite: two pairs of adjacent sides are of equal length. This implies that one diagonal divides the kite into congruent triangles, and so the angles between the two pairs of equal sides are equal in measure. It also implies that the diagonals are perpendicular. (It is common, especially in the discussions on plane tessellations, to refer to the concave quadrilateral with these properties as a dart or arrowhead, with term kite being restricted to the convex shape.)
- Orthodiagonal quadrilateral: the diagonals cross at right angles.
- Trapezium (British English) or trapezoid (American English): one pair of opposite sides are parallel.
- Isosceles trapezium (Brit.) or isosceles trapezoid (NAm.): one pair of opposite sides are parallel and the base angles are equal in measure. This implies that the other two sides are of equal length, and that the diagonals are of equal length. An alternative definition is: "a quadrilateral with an axis of symmetry bisecting one pair of opposite sides".
- Trapezium (NAm.): no sides are parallel. (In British English this would be called an irregular quadrilateral, and was once called a trapezoid.)
- Cyclic quadrilateral: the four vertices lie on a circumscribed circle. A quadrilateral is cyclic if and only if opposite angles sum to 180°.
- Tangential quadrilateral: the four edges are tangential to an inscribed circle. Another term for a tangential polygon is inscriptible.
- Bicentric quadrilateral: both cyclic and tangential.
- Ex-tangential quadrilateral: the four extensions of the sides are tangent to an excircle.
More quadrilaterals
- A geometric chevron (dart or arrowhead) is a concave quadrilateral with bilateral symmetry like a kite, but one interior angle is reflex.
- A self-intersecting quadrilateral is called variously a cross-quadrilateral, crossed quadrilateral, butterfly quadrilateral or bow-tie quadrilateral. A special case of crossed quadrilaterals are the antiparallelograms, crossed quadrilaterals in which (like a parallelogram) each pair of nonadjacent sides has equal length.
- A non-planar quadrilateral is called a skew quadrilateral. Formulas to compute its dihedral angles from the edge lengths and the angle between two adjacent edges were derived for work on the properties of molecules such as cyclobutane that contain a "puckered" ring of four atoms.[2] See skew polygon for more.
Area of a convex quadrilateral
There are various general formulas for the area K of a convex quadrilateral.
The area of a quadrilateral ABCD can be calculated using vectors. Let vectors AC and BD form the diagonals from A to C and from B to D. The area of the quadrilateral is then
which is the magnitude of the cross product of vectors AC and BD. In two-dimensional Euclidean space, expressing vector AC as a free vector in Cartesian space equal to (x1,y1) and BD as (x2,y2), this can be rewritten as:
The area can be expressed in trigonometric terms as
where the lengths of the diagonals are p and q and the angle between them is  .[3] In the case of an orthodiagonal quadrilateral e.g. rhombus, square, and kite, this formula reduces to
.[3] In the case of an orthodiagonal quadrilateral e.g. rhombus, square, and kite, this formula reduces to 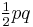 since
since  is 90°.
is 90°.
Bretschneider's formula[4] expresses the area in terms of the sides and angles:
where the sides in sequence are 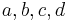 , where
, where 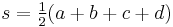 is the semiperimeter, and
is the semiperimeter, and  and
and  are any two opposite angles. This reduces to Brahmagupta's formula for the area of a cyclic quadrilateral when
are any two opposite angles. This reduces to Brahmagupta's formula for the area of a cyclic quadrilateral when 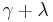 = 180°.
= 180°.
Another area formula in terms of the sides and angles, with  being between sides b and c and
being between sides b and c and  being between sides a and d (adjacent sides belonged to the angles), is
being between sides a and d (adjacent sides belonged to the angles), is
In the case of a cyclic quadrilateral, the latter formula becomes
In a parallelogram, where both pairs of opposite sides and angles are equal, this formula reduces to 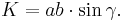
Next,[5] the following formula expresses the area in terms of the sides and diagonals:
where p and q are the diagonals. Again, this reduces to Brahmagupta's formula in the cyclic quadrilateral case, since then 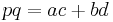 .
.
Alternatively, we can write the area in terms of the sides and the intersection angle  of the diagonals, so long as this angle is not 90°:[6]
of the diagonals, so long as this angle is not 90°:[6]
In the case of a parallelogram, the latter formula becomes
Area inequalities
If a convex quadrilateral has the consecutive sides a, b, c, d and the diagonals p, q, then its area K satisfy[7]
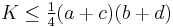 with equality only for a rectangle.
with equality only for a rectangle.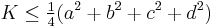 with equality only for a square.
with equality only for a square.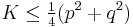 with equality only if the diagonals are perpendicular and equal.
with equality only if the diagonals are perpendicular and equal.
Euler's quadrilateral theorems
In any convex quadrilateral ABCD, the sum of the squares of the four sides is equal to the sum of the squares of the two diagonals plus four times the square of the line segment connecting the midpoints of the diagonals. Thus
where M and N are the midpoint of the diagonals AC and BD.[8]:p.126 This is sometimes known as Euler's quadrilateral theorem and is a generalization of the parallelogram law.
Euler also generalized Ptolemy's theorem, which is an equality in a cyclic quadrilateral, into an inequality for a convex quadrilateral. It states that
where there is equality if and only if the quadrilateral is cyclic.[8]:p.128-129
Miscellaneous facts about quadrilaterals in general
- The length of the diagonal that is opposite to the adjacent sides a and b at angle θ is given by
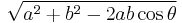 which is derived from the law of cosines.
which is derived from the law of cosines. - The midpoints of the sides of a quadrilateral are the vertices of a parallelogram called the Varignon parallelogram. The area of the Varignon parallelogram equals one-half the area of the original quadrilateral and the perimeter of the Varignon parallelogram equals the sum of the diagonals of the original quadrilateral.
- Let exterior squares be drawn on all sides of a quadrilateral. The segments connecting the centers of opposite squares are (a) equal in length, and (b) perpendicular. Thus these centers are the vertices of an orthodiagonal quadrilateral.
- The line segment joining the midpoints of two opposite sides of any quadrilateral, the segment joining the midpoints of the other two sides, and the segment joining the midpoints of the diagonals are concurrent and are all bisected by their point of intersection.[8]:p.125
- The internal bisectors of the angles of a quadrilateral form a cyclic quadrilateral.[8]:p.127
- Among all quadrilaterals with a given perimeter, the one with the largest area is the square. This is called the isoperimetric theorem for quadrilaterals.
- For any simple quadrilateral with given edge lengths, there is a cyclic quadrilateral with the same edge lengths.[9]
- The quadrilateral with given side lengths that has the maximum area is the cyclic quadrilateral.[9]
Special line segments
- The two diagonals of a convex quadrilateral are the line segments that connect opposite vertices.
- The two bimedians of a convex quadrilateral are the line segments that connect the midpoints of opposite sides.[10] They intersect at the centroid of the quadrilateral.
- The four maltitudes of a convex quadrilateral are the perpendiculars to a side through the midpoint of the opposite side.[11]
- The eight tangent lengths of a tangential quadrilateral are the line segments from a vertex to the points where the incircle is tangent to the sides. From each vertex there are two congruent tangent lengths.
- The two tangency chords of a tangential quadrilateral are the line segments that connect points on opposite sides where the incircle is tangent to these sides. These are also the diagonals of the contact quadrilateral.
Bimedians
The length of the bimedians in a convex quadrilateral with sides a, b, c, d are given by
and
where p and q are the length of the diagonals.[12] Hence[8]:p.126
This is also a corollary to the parallelogram law applied in the Varignon parallelogram, since the sides in this parallelogram are half the lengths of the diagonals of the original quadrilateral.
Taxonomy
A taxonomy of quadrilaterals is illustrated by the following graph. Lower forms are special cases of higher forms. Note that "trapezium" here is referring to the British definition (the North American equivalent is a trapezoid), and "kite" excludes the concave kite (arrowhead or dart). Inclusive definitions are used throughout.
Miscellaneous facts about special quadrilaterals
- The diagonals of a crossed or concave quadrilateral do not intersect inside the shape.
- The diagonals of a rhombus bisect the angles.
- Let ABCD be a trapezoid (in the U.S. sense of having two parallel sides) with vertices A, B, C, and D in sequence and with parallel sides AB and DC. Let E be the intersection of the diagonals, and let F be on side DA and G be on side BC such that FEG is parallel to AB and CD. Then FG is the harmonic mean of AB and DC:
- A parallelogram with equal diagonals is a rectangle.
- A cyclic quadrilateral with successive sides a, b, c, d and diagonals p, q has pq=ac+bd.
- A cyclic quadrilateral with successive vertices A, B, C, D and successive sides a=AB, b=BC, c=CD, and d=DA and with diagonals p=AC and q=BD has:
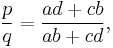
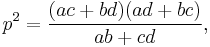 and
and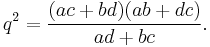
- A cyclic quadrilateral with successive sides a, b, c, d and semiperimeter s has circumradius (the radius of the circumscribing circle) given by[13]
- A parallelogram with diagonals p, q and successive sides a, b, c, and d with d=b and c=a has
- For any point P in the interior of a rectangle with successive vertices A, B, C, D, we have
- Any line through the midpoint (centroid) of a parallelogram bisects the area.
- An orthodiagonal quadrilateral (one with perpendicular diagonals) with sides a, b, c, d in sequence has[6][8]:p.136
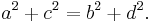
- There are no cyclic quadrilaterals with unequal rational sides in arithmetic progression and with rational area.[14]
- There are no cyclic quadrilaterals with unequal rational sides in geometric progression and with rational area.[14]
See also
- Bicentric quadrilateral
- Cyclic quadrilateral
- Ex-tangential quadrilateral
- Kite
- Orthodiagonal quadrilateral
- Parallelogram
- Rectangle
- Rhombus
- Square
- Tangential quadrilateral
- Trapezoid
References
- ^ Stars: A Second Look
- ^ M.P. Barnett and J.F. Capitani, Modular chemical geometry and symbolic calculation, International Journal of Quantum Chemistry, 106 (1) 215--227, 2006.
- ^ Harries, J. "Area of a quadrilateral," Mathematical Gazette 86, July 2002, 310-311.
- ^ R. A. Johnson, Advanced Euclidean Geometry, 2007, Dover Publ., p. 82.
- ^ E. W. Weisstein. "Bretschneider's formula". MathWorld -- A Wolfram Web Resource. http://mathworld.wolfram.com/Bretschneider'sFormula.html.
- ^ a b Mitchell, Douglas W., "The area of a quadrilateral," Mathematical Gazette 93, July 2009, 306-309.
- ^ O. Bottema, Geometric Inequalities, Wolters-Noordhoff Publishing, The Netherlands, 1969, pp. 129, 132.
- ^ a b c d e f Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
- ^ a b Thomas Peter, Maximizing the Area of a Quadrilateral, The College Mathematics Journal, Vol. 34, No. 4 (Sep., 2003), pp. 315-316.
- ^ Eric W. Weisstein, MathWorld, [1]
- ^ Eric W. Weisstein, MathWorld, [2]
- ^ Mateescu Constantin, Answer to Inequality Of Diagonal , [3]
- ^ Hoehn, Larry, "Circumradius of a cyclic quadrilateral," Mathematical Gazette 84, March 2000, 69-70.
- ^ a b Buchholz, R. H., and MacDougall, J. A. "Heron quadrilaterals with sides in arithmetic or geometric progression", Bull. Austral. Math. Soc. 59 (1999), 263-269. http://journals.cambridge.org/article_S0004972700032883
External links
- Weisstein, Eric W., "Quadrilateral" from MathWorld.
- Compendium Geometry Analytic Geometry of Quadrilaterals
- Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot
- Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref
- A (dynamic) Hierarchical Quadrilateral Tree at Dynamic Geometry Sketches
- An extended classification of quadrilaterals at Dynamic Math Learning Homepage
- Quadrilateral Venn Diagram Quadrilaterals expressed in the form of a Venn diagram, where the areas are also the shape of the quadrilateral they describe.
- The role and function of a hierarchical classification of quadrilaterals by Michael de Villiers
|
|||||||||||||||||
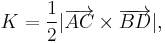
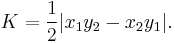
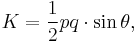
![\begin{align}
K &= \sqrt{(s-a)(s-b)(s-c)(s-d) - \tfrac{1}{2} abcd \; [ 1 %2B \cos (\gamma %2B \lambda) ]} \\
&= \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \left[ \cos^2 \left( \tfrac{\gamma %2B \lambda}{2} \right) \right]} \\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/8586e2e96b1292c02069ea10b2542417.png)