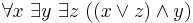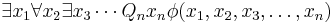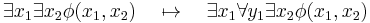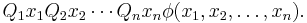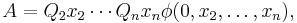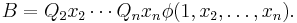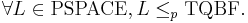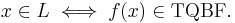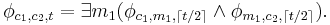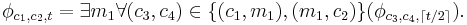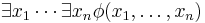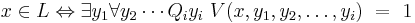True quantified Boolean formula

In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified (or bound), using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false (since there are no free variables). If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT (Quantified SAT).

1 Overview
2 Prenex normal form
3 Solving
4 PSPACE-completeness
5 Miscellany
6 Notes and references
7 See also
8 External links

Overview

In computational complexity theory, the quantified Boolean formula problem (QBF) is a generalization of the Boolean satisfiability problem in which both existential quantifiers and universal quantifiers can be applied to each variable. Put another way, it asks whether a quantified sentential form over a set of Boolean variables is true or false. For example, the following is an instance of QBF:

$\forall x\ \exists y\ \exists z\ ((x \lor z) \land y)$

QBF is the canonical complete problem for PSPACE, the class of problems solvable by a deterministic or nondeterministic Turing machine in polynomial space and unlimited time.^[1] Given the formula in the form of an abstract syntax tree, the problem can be solved easily by a set of mutually recursive procedures which evaluate the formula. Such an algorithm uses space proportional to the height of the tree, which is linear in the worst case, but uses time exponential in the number of quantifiers.

Provided that MA ⊊ PSPACE, which is widely believed, QBF cannot be solved, nor can a given solution even be verified, in either deterministic or probabilistic polynomial time (in fact, unlike the satisfiability problem, there's no known way to specify a solution succinctly). It is trivial to solve using an alternating Turing machine in linear time, which is no surprise since in fact AP = PSPACE, where AP is the class of problems alternating machines can solve in polynomial time.^[2]

When the seminal result IP = PSPACE was shown (see interactive proof system), it was done by exhibiting an interactive proof system that could solve QBF by solving a particular arithmetization of the problem.^[3]

QBF formulas have a number of useful canonical forms. For example, it can be shown that there is a polynomial-time many-one reduction that will move all quantifiers to the front of the formula and make them alternate between universal and existential quantifiers. There is another reduction that proved useful in the IP = PSPACE proof where no more than one universal quantifier is placed between each variable's use and the quantifier binding that variable. This was critical in limiting the number of products in certain subexpressions of the arithmetization.

Prenex normal form

A fully quantified Boolean formula can be assumed to have a very specific form, called prenex normal form. It has two basic parts: a portion containing only quantifiers and a portion containing an unquantified Boolean formula usually denoted as $\phi$ . If there are n Boolean variables, the entire formula can be written as

$\exists x_1 \forall x_2 \exists x_3 \cdots Q_n x_n \phi(x_1, x_2, x_3, \dots, x_n)$

where every variable falls within the scope of some quantifier. By introducing dummy variables, any formula in prenex normal form can be converted into a sentence where existential and universal quantifiers alternate. Using the dummy variable 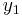$y_1$ ,

$\exists x_1 \exists x_2 \phi(x_1, x_2) \quad \mapsto \quad \exists x_1 \forall y_1 \exists x_2 \phi(x_1, x_2)$

The second sentence has the same truth value but follows the restricted syntax. Assuming fully quantified Boolean formulas to be in prenex normal form is a frequent feature of proofs.

Solving

There is a simple recursive algorithm for determining whether a TQBF is true. Given some QBF

$Q_1 x_1 Q_2 x_2 \cdots Q_n x_n \phi(x_1, x_2, \dots, x_n).$

If the formula contains no quantifiers, we can just return the formula. Otherwise, we take off the first quantifier and check both possible values for the first variable:

$A = Q_2 x_2 \cdots Q_n x_n \phi(0, x_2, \dots, x_n),$

$B = Q_2 x_2 \cdots Q_n x_n \phi(1, x_2, \dots, x_n).$

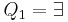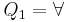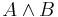If $Q_1 = \exists$ , then return $A \lor B$ . If $Q_1 = \forall$ , then return $A \land B$ .

How fast does this algorithm run? For every quantifier in the initial QBF, the algorithm makes two recursive calls on only a linearly smaller subproblem. This gives the algorithm an exponential runtime O(2^n).

How much space does this algorithm use? Within each invocation of the algorithm, it needs to store the intermediate results of computing A and B. Every recursive call takes off one quantifier, so the total recursive depth is linear in the number of quantifiers. Formulas that lack quantifiers can be evaluated in space logarithmic in the number of variables. The initial QBF was fully quantified, so there are at least as many quantifiers as variables. Thus, this algorithm uses O(n + log n) = O(n) space. This makes the TQBF language part of the PSPACE complexity class.

PSPACE-completeness

The TQBF language serves in complexity theory as the canonical PSPACE-complete problem. Being PSPACE-complete means that a language is in PSPACE and that the language is also PSPACE-hard. The algorithm above shows that TQBF is in PSPACE. Showing that TQBF is PSPACE-hard requires showing that any language in the complexity class PSPACE can be reduced to TQBF in polynomial time. I.e.,

$\forall L\in \textrm{PSPACE}, L\leq_p \textrm{TQBF}.$

This means that, for a PSPACE language L, whether an input $x$ is in L can be decided by checking whether $f(x)$ is in TQBF, for some function $f$ that is required to run in polynomial time (relative to the length of the input) Symbolically,

$x\in L\iff f(x)\in \textrm{TQBF}.$

Proving that TQBF is PSPACE-hard, requires specification of $f$ .

So, suppose that L is a PSPACE language. This means that L can be decided by a polynomial space deterministic Turing machine (DTM). This is very important for the reduction of L to TQBF, because the configurations of any such Turing Machine can be represented as Boolean formulas, with Boolean variables representing the state of the machine as well as the contents of each cell on the Turing Machine tape, with the position of the Turing Machine head encoded in the formula by the formula's ordering. 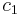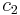In particular, our reduction will use the variables $c_1$ and $c_2$ , which represent two possible configurations of the DTM for L, and a natural number t, in constructing a QBF 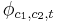$\phi_{c_1,c_2,t}$ which is true if and only if the DTM for L can go from the configuration encoded in 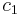$c_1$ to the configuration encoded in 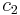$c_2$ in no more than t steps. The function $f$ , then, will construct from the DTM for L a QBF 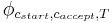$\phi_{c_{start},c_{accept},T}$ , where 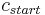$c_{start}$ is the DTM's starting configuration, 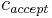$c_{accept}$ is the DTM's accepting configuration, and T is the maximum number of steps the DTM could need to move from one configuration to the other. We know that T = O(exp(n)), where n is the length of the input, because this bounds the total number of possible configurations of the relevant DTM. Of course, it cannot take the DTM more steps than there are possible configurations to reach 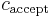$c_\mathrm{accept}$ unless it enters a loop, in which case it will never reach 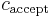$c_\mathrm{accept}$ anyway.

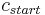At this stage of the proof, we have already reduced the question of whether an input formula $w$ (encoded, of course, in $c_{start}$ ) is in L to the question of whether the QBF 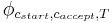$\phi_{c_{start},c_{accept},T}$ , i.e., 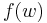$f(w)$ , is in TQBF. The remainder of this proof proves that $f$ can be computed in polynomial time.

For 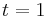$t=1$ , computation of 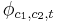$\phi_{c_1,c_2,t}$ is straightforward--either one of the configurations changes to the other in one step or it does not. Since the Turing Machine that our formula represents is deterministic, this presents no problem.

For 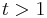$t>1$ , computation of 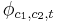$\phi_{c_1,c_2,t}$ involves a recursive evaluation, looking for a so-called "middle point" 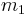$m_1$ . In this case, we rewrite the formula as follows:

$\phi_{c_1,c_2,t}=\exists m_1(\phi_{c_1,m_1,\lceil t/2\rceil}\wedge\phi_{m_1,c_2,\lceil t/2\rceil}).$

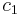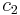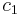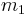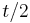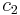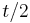This converts the question of whether $c_1$ can reach $c_2$ in t steps to the question of whether $c_1$ reaches a middle point $m_1$ in $t/2$ steps, which itself reaches $c_2$ in $t/2$ steps. The answer to the latter question of course gives the answer to the former.

Now, t is only bounded by T, which is exponential (and so not polynomial) in the length of the input. Additionally, each recursive layer virtually doubles the length of the formula. (The variable 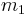$m_1$ is only one midpoint--for greater t, there are more stops along the way, so to speak.) So the time required to recursively evaluate 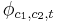$\phi_{c_1,c_2,t}$ in this manner could be exponential as well, simply because the formula could become exponentially large. 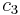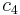This problem is solved by universally quantifying using variables $c_3$ and $c_4$ over the configuration pairs (e.g., 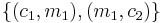$\{ (c_1,m_1),(m_1,c_2)\}$ ), which prevents the length of the formula from expanding due to recursive layers. 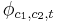This yields the following interpretation of $\phi_{c_1,c_2,t}$ :

$\phi_{c_1,c_2,t}=\exists m_1\forall (c_3,c_4)\in \{ (c_1,m_1),(m_1,c_2)\}(\phi_{c_3,c_4,\lceil t/2\rceil}).$

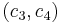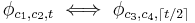This version of the formula can indeed be computed in polynomial time, since any one instance of it can be computed in polynomial time. The universally quantified ordered pair simply tells us that whichever choice of $(c_3,c_4)$ is made, $\phi_{c_1,c_2,t}\iff\phi_{c_3,c_4,\lceil t/2\rceil}$ .

Thus, 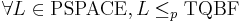$\forall L\in \textrm{PSPACE}, L\leq_p \textrm{TQBF}$ , so TQBF is PSPACE-hard. Together with the above result that TQBF is in PSPACE, this completes the proof that TQBF is a PSPACE-complete language.

(This proof follows Sipser 2006 pp. 310-313 in all essentials. Papadimitriou 1994 also includes a proof.)

Miscellany

One important subproblem in TQBF is the Boolean satisfiability problem. In this problem, you wish to know whether a given Boolean formula $\phi$ can be made true with some assignment of variables. This is equivalent to the TQBF using only existential quantifiers:

$\exists x_1 \cdots \exists x_n \phi(x_1, \ldots, x_n)$

This is also an example of the larger result NP 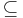$\subseteq$ PSPACE which follows directly from the observation that a polynomial time verifier for a proof of a language accepted by a NTM (Non-deterministic Turing machine) requires polynomial space to store the proof.

Any class in the polynomial hierarchy (PH) has TQBF as its complete problem. In other words, for the class comprising all languages L for which there exists a poly-time TM V, a verifier, such that for all input x and some constant i,

$x \in L \Leftrightarrow \exists y_1 \forall y_2 \cdots Q_i y_i \ V(x,y_1,y_2,\dots,y_i)\ =\ 1$

which has a specific QBF formulation that is given as

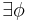$\exists \phi$ such that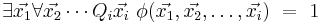 $\exists \vec{x_1} \forall \vec{x_2} \cdots Q_i \vec{x_i}\ \phi(\vec{x_1},\vec{x_2},\dots,\vec{x_i})\ =\ 1$

where the 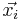$\vec{x_i}$ 's are vectors of Boolean variables.

It is important to note that while TQBF the language is defined as the collection of true quantified Boolean formulas, the abbreviation TQBF is often used (even in this article) to stand for a totally quantified Boolean formula, often simply called a QBF (quantified Boolean formula, understood as "fully" or "totally" quantified). It is important to distinguish contextually between the two uses of the abbreviation TQBF in reading the literature.
A TQBF can be thought of as a game played between two players, with alternating moves. Existentially quantified variables are equivalent to the notion that a move is available to a player at a turn. Universally quantified variables mean that the outcome of the game does not depend on what move a player makes at that turn. Also, a TQBF whose first quantifier is existential corresponds to a formula game in which the first player has a winning strategy.
A TQBF for which the quantified formula is in 2-CNF may be solved in linear time, by an algorithm involving strong connectivity analysis of its implication graph. The 2-satisfiability problem is a special case of TQBF for these formulas, in which every quantifier is existential.^[4]^[5]
There is a systematic treatment of restricted versions of quantified boolean formulas (giving Schaefer-type classifications) provided in an expository paper by Hubie Chen.^[6]

Notes and references

^ M. Garey and D. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman, San Francisco, California. ISBN 0-7167-1045-5.
^ A. Chandra, D. Kozen, and L. Stockmeyer (1981). "Alternation". Journal of the ACM 28 (1): 114–133. doi:10.1145/322234.322243. http://portal.acm.org/citation.cfm?id=322243.
^ Adi Shamir (1992). "Ip = Pspace". Journal of the ACM 39 (4): 869–877. doi:10.1145/146585.146609. http://portal.acm.org/citation.cfm?doid=146585.146609.
^ Krom, Melven R. (1967). "The Decision Problem for a Class of First-Order Formulas in Which all Disjunctions are Binary". Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 13: 15–20. doi:10.1002/malq.19670130104 .
^ Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E. (1979). "A linear-time algorithm for testing the truth of certain quantified boolean formulas". Information Processing Letters 8 (3): 121–123. doi:10.1016/0020-0190(79)90002-4. http://www.math.ucsd.edu/~sbuss/CourseWeb/Math268_2007WS/2SAT.pdf .
^ Chen, Hubie (December 2009). "A Rendezvous of Logic, Complexity, and Algebra". ACM Computing Surveys (ACM) 42 (1): 1. doi:10.1145/1592451.1592453.

Fortnow & Homer (2003) provides some historical background for PSPACE and TQBF.
Zhang (2003) provides some historical background of Boolean formulas.
Arora, Sanjeev. (2001). COS 522: Computational Complexity. Lecture Notes, Princeton University. Retrieved October 10, 2005.
Fortnow, Lance & Steve Homer. (2003, June). A short history of computational complexity. The Computational Complexity Column, 80. Retrieved October 9, 2005.
Papadimitriou, C. H. (1994). Computational Complexity. Reading: Addison-Wesley.
Sipser, Michael. (2006). Introduction to the Theory of Computation. Boston: Thomson Course Technology.
Zhang, Lintao. (2003). Searching for truth: Techniques for satisfiability of boolean formulas. Retrieved October 10, 2005.

External links

The Quantified Boolean Formulas Library (QBFLIB)