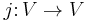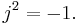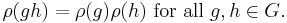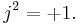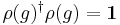Quaternionic representation

In mathematical field of representation theory, a quaternionic representation is a representation on a complex vector space V with an invariant quaternionic structure, i.e., an antilinear equivariant map

j\colon V\to V\,

which satisfies

j^2=-1.\,

Together with the imaginary unit i and the antilinear map k := ij, j equips V with the structure of a quaternionic vector space (i.e., V becomes a module over the division algebra of quaternions). From this point of view, quaternionic representation of a group G is a group homomorphism φ: G → GL(V, H), the group of invertible quaternion-linear transformations of V. In particular, a quaternionic matrix representation of g assigns a square matrix of quaternions ρ(g) to each element g of G such that ρ(e) is the identity matrix and

\rho(gh)=\rho(g)\rho(h)\text{ for all }g, h \in G.\,

Quaternionic representations of associative and Lie algebras can be defined in a similar way.

Contents

Properties and related concepts

If V is a unitary representation and the quaternionic structure j is a unitary operator, then V admits an invariant complex symplectic form ω, and hence is a symplectic representation. This always holds if V is a representation of a compact group (e.g. a finite group) and in this case quaternionic representations are also known as symplectic representations. Such representations, amongst irreducible representations, can be picked out by the Frobenius-Schur indicator.

Quaternionic representations are similar to real representations in that they are isomorphic to their complex conjugate representation. Here a real representation is taken to be a complex representation with an invariant real structure, i.e., an antilinear equivariant map

j\colon V\to V\,

which satisfies

j^2=%2B1.\,

A representation which is isomorphic to its complex conjugate, but which is not a real representation, is sometimes called a pseudoreal representation.

Real and pseudoreal representations of a group G can be understood by viewing them as representations of the real group algebra R[G]. Such a representation will be a direct sum of central simple R-algebras, which, by the Artin-Wedderburn theorem, must be matrix algebras over the real numbers or the quaternions. Thus a real or pseudoreal representation is a direct sum of irreducible real representations and irreducible quaternionic representations. It is real if no quaternionic representations occur in the decomposition.

Examples

A common example involves the quaternionic representation of rotations in three dimensions. Each (proper) rotation is represented by a quaternion with unit norm. There is an obvious one-dimensional quaternionic vector space, namely the space H of quaternions themselves under left multiplication. By restricting this to the unit quaternions, we obtain a quaternionic representation of the spinor group Spin(3).

This representation ρ: Spin(3) → GL(1,H) also happens to be a unitary quaternionic representation because

\rho(g)^\dagger \rho(g)=\mathbf{1}\,

for all g in Spin(3).

Another unitary example is the spin representation of Spin(5). An example of a nonunitary quaternionic representation would be the two dimensional irreducible representation of Spin(5,1).

More generally, the spin representations of Spin(d) are quaternionic when d equals 3 + 8k, 4 + 8k, and 5 + 8k dimensions, where k is an integer. In physics, one often encounters the spinors of Spin(d, 1). These representations have the same type of real or quaternionic structure as the spinors of Spin(d − 1).

Among the compact real forms of the simple Lie groups, irreducible quaternionic representations only exist for the Lie groups of type A4k+1, B4k+1, B4k+2, Ck, D4k+2, and E7.

References

See also