Pseudoisotopy theorem
In mathematics, the pseudoisotopy theorem is a theorem of Jean Cerf's[1] which refers to the connectivity of a group of diffeomorphisms of a manifold.
Statement
Given a differentiable manifold M (with or without boundary), a pseudo-isotopy diffeomorphism of M is a diffeomorphism of M × [0, 1] which restricts to the identity on ![M \times \{0\} \cup \partial M \times [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/0d7628cc1bb2165272cb64779ef742a1.png) .
.
Given ![f�: M \times [0,1] \to M \times [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/2a95ec86d984d6275e3539310dc9d85d.png) a pseudo-isotopy diffeomorphism, its restriction to
a pseudo-isotopy diffeomorphism, its restriction to 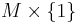 is a diffeomorphism
is a diffeomorphism  of M. We say g is pseudo-isotopic to the identity. One should think of a pseudo-isotopy as something that is almost an isotopy -- the obstruction to ƒ being an isotopy of g to the identity is whether or not ƒ preserves the level-sets
of M. We say g is pseudo-isotopic to the identity. One should think of a pseudo-isotopy as something that is almost an isotopy -- the obstruction to ƒ being an isotopy of g to the identity is whether or not ƒ preserves the level-sets 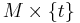 for
for ![t \in [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/d9a06fde4663cdd5b1ba693e9127232f.png) .
.
Cerf's theorem states that, provided M is simply-connected and dim(M) ≥ 5, the group of pseudo-isotopy diffeomorphisms of M is connected. Equivalently, a diffeomorphism of M is isotopic to the identity if and only if it is pseudo-isotopic to the identity. [2]
Relation to Cerf theory
The starting point of the proof is to think of the height function as a 1-parameter family of smooth functions on M by considering the function ![\pi_{[0,1]} \circ f_t](/2012-wikipedia_en_all_nopic_01_2012/I/4f68b335265d244e212f6da0fc1218f0.png) . One then applies Cerf theory [3].
. One then applies Cerf theory [3].
References
- ^ French mathematician, born 1928.[1]
- ^ J.Cerf, La stratification naturelle des espaces de fonctions deff\'erentiables r\'eelles et le th\'eor\`eme de la pseudo-isotopie, Inst. Hautes \'Etudes Sci. Publ. Math. No {\bf 39} (1970) 5–173.
- ^ J.Cerf, La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie, Inst. Hautes Études Sci. Publ. Math. No. 39 (1970) 5–173.