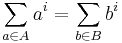Prouhet–Tarry–Escott problem
In mathematics, the Prouhet–Tarry–Escott problem asks for two disjoint sets A and B of n integers each, such that:
for each integer i from 1 to a given k.[1]
This problem was named after Eugène Prouhet, who studied it in the early 1850s, and Gaston Tarry and Escott, who studied it in the early 1910s.
The largest value of k for which a solution with n = k+1 is known is given by A = {±22, ±61, ±86, ±127, ±140, ±151}, B = {±35, ±47, ±94, ±121, ±146, ±148} for which k = 11.
Contents |
Example
For example, a solution with n = 6 and k = 5 is the two sets { 0, 5, 6, 16, 17, 22 } and { 1, 2, 10, 12, 20, 21 }, because:
- 01 + 51 + 61 + 161 + 171 + 221 = 11 + 21 + 101 + 121 + 201 + 211
- 02 + 52 + 62 + 162 + 172 + 222 = 12 + 22 + 102 + 122 + 202 + 212
- 03 + 53 + 63 + 163 + 173 + 223 = 13 + 23 + 103 + 123 + 203 + 213
- 04 + 54 + 64 + 164 + 174 + 224 = 14 + 24 + 104 + 124 + 204 + 214
- 05 + 55 + 65 + 165 + 175 + 225 = 15 + 25 + 105 + 125 + 205 + 215.
See also
Notes
References
- Borwein, Peter B. (2002), "The Prouhet–Tarry–Escott problem", Computational Excursions in Analysis and Number Theory, CMS Books in Mathematics, Springer-Verlag, pp. 85–96, ISBN 0-387-95444-9, http://books.google.com/?id=A_ITwN13J6YC&pg=85#PPA85,M1, retrieved 2009-06-16 Chap.11.