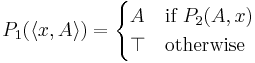Propositional proof system
In propositional calculus and proof complexity a propositional proof system (pps), also called a Cook–Reckhow propositional proof system, is system for proving classical propositional tautologies.
Contents |
Mathematical definition
Formally a pps is a polynomial-time function P whose range is the set of all propositional tautologies (denoted TAUT).[1] If A is a formula, then any x such that P(x) = A is called a P-proof of A. The condition defining pps can be broken up as follows:
- Completeness: every propositional tautology has a P-proof,
- Soundness: if a propositional formula has a P-proof then it is a tautology,
- Efficiency: P runs in polynomial time.
In general, a proof system for a language L is a polynomial-time function whose range is L. Thus, a propositional proof system is a proof system for TAUT.
Sometimes the following alternative definition is considered: a pps is given as a proof-verification algorithm P(A,x) with two inputs. If P accepts the pair (A,x) we say that x is a P-proof of A. P is required to run in polynomial time, and moreover, it must hold that A has a P-proof if and only if it is a tautology.
If P1 is a pps according to the first definition, then P2 defined by P2(A,x) if and only if P1(x) = A is a pps according to the second definition. Conversely, if P2 is a pps according to the second definition, then P1 defined by
(P1 takes pairs as input) is a pps according to the first definition, where 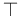 is a fixed tautology.
is a fixed tautology.
History
Historically, Frege's propositional calculus was the first propositional proof system. The general definition of a propositional proof system is due to Stephen Cook and Robert A. Reckhow (1979).[1]
Relation with computational complexity theory
Propositional proof system can be compared using the notion of p-simulation. A propositional proof system P p-simulates Q (written as P ≤pQ) when there is a polynomial-time function F such that P(F(x)) = Q(x) for every x.[1] That is, given a Q-proof x, we can find in polynomial time a P-proof of the same tautology. If P ≤pQ and Q ≤pP, the proof systems P and Q are p-equivalent. There is also a weaker notion of simulation: a pps P simulates a pps Q if there is a polynomial p such that for every Q-proof x of a tautology A, there is a P-proof y of A such that the length of y, |y| is at most p(|x|). (Some authors use the words p-simulation and simulation interchangeably for either of these two concepts, usually the latter.)
A propositional proof system is called p-optimal if it p-simulates all other propositional proof systems, and it is optimal if it simulates all other pps. A propositional proof system P is polynomially bounded (also called super) if every tautology has a short (i.e., polynomial-size) P-proof.
If P is polynomially bounded and Q simulates P, then Q is also polynomially bounded.
The set of propositional tautologies is a coNP-complete. A propositional proof system is a certificate-verifier for membership in TAUT. Existence of a polynomially bounded propositional proof system means that there is a verifier with polynomial-size certificates, i.e., TAUT is in NP. In fact these two statements are equivalent, i.e., there is a polynomially bounded propositional proof system if and only if the complexity classes NP and coNP are equal.[1]
Examples of propositional proof systems
Some examples of propositional proof systems studied are:
- Resolution and various extensions of it like DPLL algorithm
- Natural deduction
- Sequent calculus
- Frege system
- Extended Frege
- Polynomial calculus
- Nullstellensatz system
- Cutting-plane method
References
- ^ a b c d Cook, Stephen; Reckhow, Robert A. (1979). "The Relative Efficiency of Propositional Proof Systems". Journal of Symbolic Logic 44 (1): pp. 36–50. http://www.jstor.org/stable/2273702.
Further reading
- Samuel Buss (1998), "An introduction to proof theory", in: Handbook of Proof Theory (ed. S.R.Buss), Elsevier (1998).
- P. Pudlák (1998), "The lengths of proofs", in: Handbook of Proof Theory (ed. S.R.Buss), Elsevier, (1998).
- P. Beame and T. Pitassi (1998). Propositional proof complexity: past, present and future. Technical Report TR98-067, Electronic Colloquium on Computational Complexity.
- Nathan Segerlind (2007) "The Complexity of Propositional Proofs", Bulletin of Symbolic Logic 13(4): 417–481
- J. Krajíček (1995), Bounded Arithmetic, Propositional Logic, and Complexity Theory, Cambridge University Press.
- J. Krajíček, Proof complexity, in: Proc. 4th European congress of mathematics (ed. A. Laptev), EMS, Zurich, pp. 221–231, (2005).
- J. Krajíček, Propositional proof complexity I. and Proof complexity and arithmetic.
- Stephen Cook and Phuong Nguyen, Logical Foundations of Proof Complexity, Cambridge University Press, 2010 (draft from 2008)