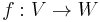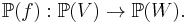Projectivization

In mathematics, projectivization is a procedure which associates to a non-zero vector space V its associated projective space 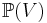${\Bbb P}(V)$ , whose elements are one-dimensional subspaces of V. More generally, any subset S of V closed under scalar multiplication defines a subset of 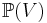${\Bbb P}(V)$ formed by the lines contained in S and called the projectivization of S.

Properties

Projectivization is a special case of the factorization by a group action: the projective space 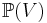${\Bbb P}(V)$ is the quotient of the open set V\{0} of nonzero vectors by the action of the multiplicative group of the base field by scalar transformations. The dimension of 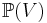${\Bbb P}(V)$ in the sense of algebraic geometry is one less than the dimension of the vector space V.

Projectivization is functorial with respect to injective linear maps: if

$f: V\to W$

is a linear map with trivial kernel then f defines an algebraic map of the corresponding projective spaces,

$\mathbb{P}(f): \mathbb{P}(V)\to \mathbb{P}(W).$

In particular, the general linear group GL(V) acts on the projective space 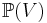${\Bbb P}(V)$ by automorphisms.

Projective completion

A related procedure embeds a vector space V over a field K into the projective space 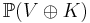${\Bbb P}(V\oplus K)$ of the same dimension. To every vector v of V, it associates the line spanned by the vector (v,1) of V⊕K.

Generalization

Main article: Proj construction

In algebraic geometry, there is a procedure that associates a projective variety Proj S with a graded commutative algebra S (under some technical restrictions on S). If S is the algebra of polynomial functions on a vector space V then Proj S is 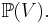${\Bbb P}(V).$ This Proj construction gives rise to a contravariant functor from the category of graded commutative rings and surjective graded maps to the category of projective schemes.