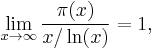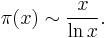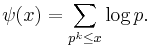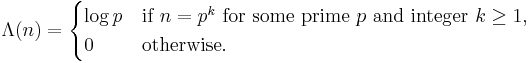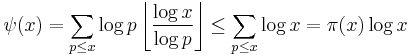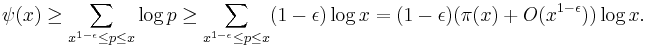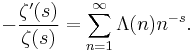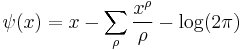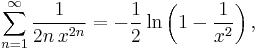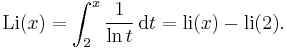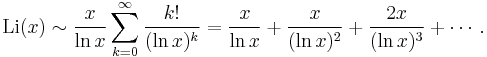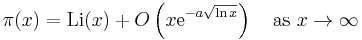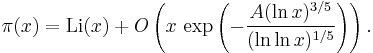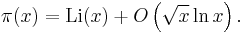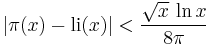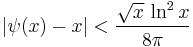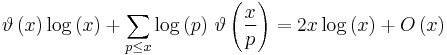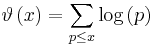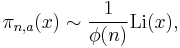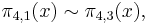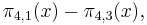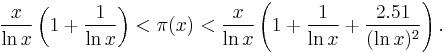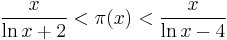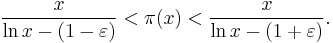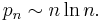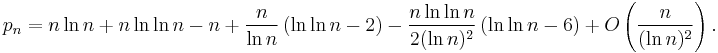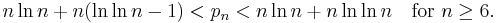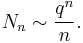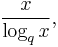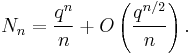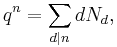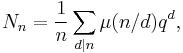Prime number theorem

In number theory, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers.

Informally speaking, the prime number theorem states that if a random integer is selected near to some large integer N, the probability that the selected integer is prime is about 1 / ln(N), where ln(N) denotes the natural logarithm of N. For example, near N = 1,000, about one in seven numbers is prime, whereas near N = 10,000,000,000, about one in 23 numbers is prime. In other words, the average gap between consecutive prime numbers near N is roughly ln(N).^[1]

1 Statement of the theorem
2 History of the asymptotic law of distribution of prime numbers and its proof
3 Proof methodology
4 Proof sketch
5 Prime-counting function in terms of the logarithmic integral
6 Elementary proofs
7 Computer verifications
8 Prime number theorem for arithmetic progressions
9 Bounds on the prime-counting function
10 Approximations for the nth prime number
11 Table of π(x), x / ln x, and li(x)
12 Analogue for irreducible polynomials over a finite field
13 See also
14 Notes
15 References
16 External links

Statement of the theorem

Let π(x) be the prime-counting function that gives the number of primes less than or equal to x, for any real number x. For example, π(10) = 4 because there are four prime numbers (2, 3, 5 and 7) less than or equal to 10. The prime number theorem then states that the limit of the quotient of the two functions π(x) and x / ln(x) as x approaches infinity is 1, which is expressed by the formula

$\lim_{x\to\infty}\frac{\pi(x)}{x/\ln(x)}=1,$

known as the asymptotic law of distribution of prime numbers. Using asymptotic notation this result can be restated as

$\pi(x)\sim\frac{x}{\ln x}.\!$

This notation (and the theorem) does not say anything about the limit of the difference of the two functions as x approaches infinity. (Indeed, the behavior of this difference is very complicated and related to the Riemann hypothesis.) Instead, the theorem states that x/ln(x) approximates π(x) in the sense that the relative error of this approximation approaches 0 as x approaches infinity.

The prime number theorem is equivalent to the statement that the nth prime number p_n is approximately equal to n ln(n), again with the relative error of this approximation approaching 0 as n approaches infinity.

History of the asymptotic law of distribution of prime numbers and its proof

Based on the tables by Anton Felkel and Jurij Vega, Adrien-Marie Legendre conjectured in 1797 or 1798 that π(a) is approximated by the function a/(A ln(a)+B), where A and B are unspecified constants. In the second edition of his book on number theory (1808) he then made a more precise conjecture, with A=1 and B= -1.08366. Carl Friedrich Gauss considered the same question: "Ins Jahr 1792 oder 1793", according to his own recollection nearly sixty years later in a letter to Encke (1849), he wrote in his logarithm table (he was then 15 or 16) the short note "Primzahlen unter 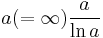$a(=\infty) \frac a{\ln a}$ ". But Gauss never published this conjecture. In 1838 Johann Peter Gustav Lejeune Dirichlet came up with his own approximating function, the logarithmic integral li(x) (under the slightly different form of a series, which he communicated to Gauss). Both Legendre's and Dirichlet's's formulas imply the same conjectured asymptotic equivalence of π(x) and x / ln(x) stated above, although it turned out that Dirichlet's approximation is considerably better if one considers the differences instead of quotients.

In two papers from 1848 and 1850, the Russian mathematician Pafnuty L'vovich Chebyshev attempted to prove the asymptotic law of distribution of prime numbers. His work is notable for the use of the zeta function ζ(s) (for real values of the argument "s", as are works of Leonhard Euler, as early as 1737) predating Riemann's celebrated memoir of 1859, and he succeeded in proving a slightly weaker form of the asymptotic law, namely, that if the limit of π(x)/(x/ln(x)) as x goes to infinity exists at all, then it is necessarily equal to one.^[2] He was able to prove unconditionally that this ratio is bounded above and below by two explicitly given constants near to 1 for all x.^[3] Although Chebyshev's paper did not prove the Prime Number Theorem, his estimates for π(x) were strong enough for him to prove Bertrand's postulate that there exists a prime number between n and 2n for any integer n ≥ 2.

Without doubt, the single most significant paper concerning the distribution of prime numbers was Riemann's 1859 memoir On the Number of Primes Less Than a Given Magnitude, the only paper he ever wrote on the subject. Riemann introduced revolutionary ideas into the subject, the chief of them being that the distribution of prime numbers is intimately connected with the zeros of the analytically extended Riemann zeta function of a complex variable. In particular, it is in this paper of Riemann that the idea to apply methods of complex analysis to the study of the real function π(x) originates. Extending these deep ideas of Riemann, two proofs of the asymptotic law of the distribution of prime numbers were obtained independently by Hadamard and de la Vallée Poussin and appeared in the same year (1896). Both proofs used methods from complex analysis, establishing as a main step of the proof that the Riemann zeta function ζ(s) is non-zero for all complex values of the variable s that have the form s = 1 + it with t > 0.^[4]

During the 20th century, the theorem of Hadamard and de la Vallée-Poussin also became known as the Prime Number Theorem. Several different proofs of it were found, including the "elementary" proofs of Atle Selberg and Paul Erdős (1949). While the original proofs of Hadamard and de la Vallée-Poussin are long and elaborate, and later proofs have introduced various simplifications through the use of Tauberian theorems but remained difficult to digest, a surprisingly short proof was discovered in 1980 by American mathematician Donald J. Newman.^[5]^[6] Newman's proof is arguably the simplest known proof of the theorem, although it is non-elementary in the sense that it uses Cauchy's integral theorem from complex analysis.

Proof methodology

In a lecture on prime numbers for a general audience, Fields medalist Terence Tao described one approach to proving the prime number theorem in poetic terms: listening to the "music" of the primes. We start with a "sound wave" that is "noisy" at the prime numbers and silent at other numbers; this is the von Mangoldt function. Then we analyze its notes or frequencies by subjecting it to a process akin to Fourier transform; this is the Mellin transform. Then we prove, and this is the hard part, that certain "notes" cannot occur in this music. This exclusion of certain notes leads to the statement of the prime number theorem. According to Tao, this proof yields much deeper insights into the distribution of the primes than the "elementary" proofs discussed below.^[7]

Proof sketch

Here is a sketch of the proof referred to in Tao's lecture mentioned above. Like most proofs of the PNT, it starts out by reformulating the problem in terms of a less intuitive, but better-behaved, prime-counting function. The idea is to count the primes (or a related set such as the set of prime powers) with weights to arrive at a function with smoother asymptotic behavior. The most common such generalized counting function is the Chebyshev function 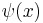$\psi(x)$ , defined by

$\psi(x) = \sum_{p^k \le x} \log p.$

Here the summation is over all prime powers up to x. This is sometimes written as 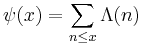$\psi(x)=\sum_{n\le x} \Lambda(n)$ , where 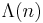$\Lambda(n)$ is the von Mangoldt function, namely

$\Lambda(n) = \begin{cases} \log p & \text{if }n=p^k \text{ for some prime } p \text{ and integer } k \ge 1, \\ 0 & \text{otherwise.} \end{cases}$

It is now relatively easy to check that the PNT is equivalent to the claim that 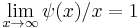$\lim_{x\to\infty} \psi(x)/x=1$ . Indeed, this follows from the easy estimates

$\psi(x) = \sum_{p\le x} \log p \left\lfloor \frac{\log x}{\log p} \right\rfloor \le \sum_{p\le x} \log x = \pi(x)\log x$

and (using big O notation) for any ε > 0,

$\psi(x) \ge \sum_{x^{1-\epsilon}\le p\le x} \log p\ge\sum_{x^{1-\epsilon}\le p\le x}(1-\epsilon)\log x=(1-\epsilon)(\pi(x)%2BO(x^{1-\epsilon}))\log x.$

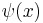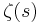The next step is to find a useful representation for $\psi(x)$ . Let $\zeta(s)$ be the Riemann zeta function. It can be shown that 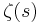$\zeta(s)$ is related to the von Mangoldt function 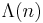$\Lambda(n)$ , and hence to 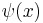$\psi(x)$ , via the relation

$-\frac{\zeta'(s)}{\zeta(s)} = \sum_{n = 1}^\infty \Lambda(n) n^{-s}.$

A delicate analysis of this equation and related properties of the zeta function, using the Mellin transform and Perron's formula, shows that for non-integer x the equation

$\psi(x) = x - \sum_{\rho} \frac{x^\rho}{\rho} - \log(2\pi)$

holds, where the sum is over all zeros (trivial and non-trivial) of the zeta function. This striking formula is one of the so-called explicit formulas of number theory, and is already suggestive of the result we wish to prove, since the term x (claimed to be the correct asymptotic order of 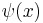$\psi(x)$ ) appears on the right-hand side, followed by (presumably) lower-order asymptotic terms.

The next step in the proof involves a study of the zeros of the zeta function. The trivial zeros −2, −4, −6, −8, ... can be handled separately:

$\sum_{n=1}^\infty \frac{1}{2n\,x^{2n}} = -\frac{1}{2}\ln\left(1-\frac{1}{x^2}\right),$

which vanishes for a large x. The nontrivial zeros, namely those on the critical strip 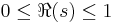$0\le \Re(s)\le 1$ , can potentially be of an asymptotic order comparable to the main term x if 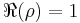$\Re(\rho)=1$ , so we need to show that all zeros have real part strictly less than 1.

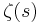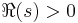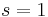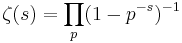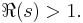To do this, we take for granted that $\zeta(s)$ is meromorphic in the half-plane $\Re(s)>0$ , and is analytic there except for a simple pole at $s=1$ , and that there is a product formula $\zeta(s)=\prod_p(1-p^{-s})^{-1}$ for $\Re(s)>1.$ This product formula follows from the existence of unique prime factorization of integers, and shows that 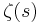$\zeta(s)$ is never zero in this region, so that its logarithm is defined there and 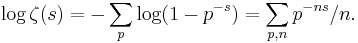$\log\zeta(s)=-\sum_p\log (1-p^{-s} )=\sum_{p,n}p^{-ns}/n.$ Write $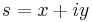s=x%2Biy$ ; then

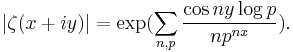
$|\zeta(x%2Biy)|=\exp(\sum_{n,p}\frac{\cos ny\log p}{np^{nx}}).$

Now observe the identity 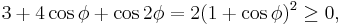$3%2B4\cos\phi%2B\cos2\phi=2(1%2B\cos\phi)^2\ge 0,$ so that

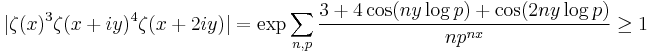
$|\zeta(x)^3\zeta(x%2Biy)^4\zeta(x%2B2iy)|=\exp\sum_{n,p}\frac{3%2B4\cos(ny\log p) %2B\cos (2ny\log p)}{np^{nx}}\ge 1$

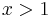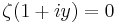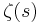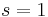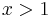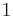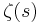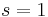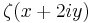for all $x> 1$ . Suppose now that $\zeta(1%2Biy)=0$ . Certainly $y$ is not zero, since $\zeta(s)$ has a simple pole at $s=1$ . Suppose that $x>1$ and let $x$ tend to $1$ from above. Since $\zeta(s)$ has a simple pole at $s=1$ and $\zeta(x%2B2iy)$ stays analytic, the left hand side in the previous inequality tends to $0$ , a contradiction.

Finally, we can conclude that the PNT is "morally" true. To rigorously complete the proof there are still serious technicalities to overcome, due to the fact that the summation over zeta zeros in the explicit formula for 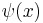$\psi(x)$ does not converge absolutely but only conditionally and in a "principal value" sense. There are several ways around this problem but all of them require rather delicate complex-analytic estimates that are beyond the scope of this article. Edwards's book^[8] provides the details.

Prime-counting function in terms of the logarithmic integral

In a handwritten note on a reprint of his 1838 paper "Sur l'usage des séries infinies dans la théorie des nombres", which he mailed to Carl Friedrich Gauss, Johann Peter Gustav Lejeune Dirichlet conjectured (under a slightly different form appealing to a series rather than an integral) that an even better approximation to π(x) is given by the offset logarithmic integral function Li(x), defined by

$\mathrm{Li}(x) = \int_2^x \frac1{\ln t} \,\mathrm{d}t = \mathrm{li}(x) - \mathrm{li}(2).$

Indeed, this integral is strongly suggestive of the notion that the 'density' of primes around t should be 1/lnt. This function is related to the logarithm by the asymptotic expansion

$\mathrm{Li}(x) \sim \frac{x}{\ln x} \sum_{k=0}^\infty \frac{k!}{(\ln x)^k} = \frac{x}{\ln x} %2B \frac{x}{(\ln x)^2} %2B \frac{2x}{(\ln x)^3} %2B \cdots.$

So, the prime number theorem can also be written as π(x) ~ Li(x). In fact, it follows from the proof of Hadamard and de la Vallée Poussin that

$\pi(x)={\rm Li} (x) %2B O \left(x \mathrm{e}^{-a\sqrt{\ln x}}\right) \quad\text{as } x \to \infty$

for some positive constant a, where O(…) is the big O notation. This has been improved to

$\pi(x)={\rm Li} (x) %2B O \left(x \, \exp \left( -\frac{A(\ln x)^{3/5}}{(\ln \ln x)^{1/5}} \right) \right).$

Because of the connection between the Riemann zeta function and π(x), the Riemann hypothesis has considerable importance in number theory: if established, it would yield a far better estimate of the error involved in the prime number theorem than is available today. More specifically, Helge von Koch showed in 1901^[9] that, if and only if the Riemann hypothesis is true, the error term in the above relation can be improved to

$\pi(x) = {\rm Li} (x) %2B O\left(\sqrt x \ln x\right).$

The constant involved in the big O notation was estimated in 1976 by Lowell Schoenfeld:^[10] assuming the Riemann hypothesis,

$|\pi(x)-{\rm li}(x)|<\frac{\sqrt x\,\ln x}{8\pi}$

for all x ≥ 2657. He also derived a similar bound for the Chebyshev prime-counting function ψ:

$|\psi(x)-x|<\frac{\sqrt x\,\ln^2 x}{8\pi}$

for all x ≥ 73.2.

The logarithmic integral Li(x) is larger than π(x) for "small" values of x. This is because it is (in some sense) counting not primes, but prime powers, where a power pⁿ of a prime p is counted as 1/n of a prime. This suggests that Li(x) should usually be larger than π(x) by roughly Li(x^1/2)/2, and in particular should usually be larger than π(x). However, in 1914, J. E. Littlewood proved that this is not always the case. The first value of x where π(x) exceeds Li(x) is probably around x = 10³¹⁶; see the article on Skewes' number for more details.

Elementary proofs

In the first half of the twentieth century, some mathematicians (notably G. H. Hardy) believed that there exists a hierarchy of proof methods in mathematics depending on what sorts of numbers (integers, reals, complex) a proof requires, and that the prime number theorem (PNT) is a "deep" theorem by virtue of requiring complex analysis.^[11] This belief was somewhat shaken by a proof of the PNT based on Wiener's tauberian theorem, though this could be set aside if Wiener's theorem were deemed to have a "depth" equivalent to that of complex variable methods. There is no rigorous and widely accepted definition of the notion of elementary proof in number theory. One definition is "a proof that can be carried out in first order Peano arithmetic." There are theorems of Peano arithmetic (for example, the Paris-Harrington theorem) provable using second order but not first order methods, but such theorems are rare to date.

In March 1948, Atle Selberg established, by elementary means, the asymptotic formula

$\vartheta \left( x \right)\log \left( x \right) %2B \sum\limits_{p \le x} {\log \left( p \right)}\ \vartheta \left( {\frac{x}{p}} \right) = 2x\log \left( x \right) %2B O\left( x \right)$

where

$\vartheta \left( x \right) = \sum\limits_{p \le x} {\log \left( p \right)}$

for primes $p$ . By July of that year, Selberg and Paul Erdős had each obtained elementary proofs of the PNT, both using Selberg's asymptotic formula as a starting point.^[11]^[12] These proofs effectively laid to rest the notion that the PNT was "deep," and showed that technically "elementary" methods (in other words Peano arithmetic) were more powerful than had been believed to be the case. 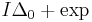In 1994, Charalambos Cornaros and Costas Dimitracopoulos proved the PNT using only $I\Delta_0%2B\exp$ ,^[13] a formal system far weaker than Peano arithmetic. On the history of the elementary proofs of the PNT, including the Erdős–Selberg priority dispute, see Dorian Goldfeld.^[11]

Computer verifications

In 2005, Avigad et al. employed the Isabelle theorem prover to devise a computer-verified variant of the Erdős–Selberg proof of the PNT.^[14] This was the first machine-verified proof of the PNT. Avigad chose to formalize the Erdős-Selberg proof rather than an analytic one because while Isabelle's library at the time could implement the notions of limit, derivative, and transcendental function, it had almost no theory of integration to speak of (Avigad et al. p. 19).

In 2009, John Harrison employed HOL Light to formalize a proof employing complex analysis.^[15] By developing the necessary analytic machinery, including the Cauchy integral formula, Harrison was able to formalize “a direct, modern and elegant proof instead of the more involved ‘elementary’ Erdös-Selberg argument.”

Prime number theorem for arithmetic progressions

Let 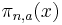$\pi_{n,a}(x)$ denote the number of primes in the arithmetic progression a, a + n, a + 2n, a + 3n, … less than x. Dirichlet and Legendre conjectured, and Vallée-Poussin proved, that, if a and n are coprime, then

$\pi_{n,a}(x) \sim \frac{1}{\phi(n)}\mathrm{Li}(x),$

where φ(·) is the Euler's totient function. In other words, the primes are distributed evenly among the residue classes [a] modulo n with gcd(a, n) = 1. This can be proved using similar methods used by Newman for his proof of the prime number theorem.^[16]

Although we have in particular

$\pi_{4,1}(x) \sim \pi_{4,3}(x), \,$

empirically the primes congruent to 3 are more numerous and are nearly always ahead in this "prime number race"; the first reversal occurs at x = 26,861.^[17]^:1–2 However Littlewood showed in 1914^[17]^:2 that there are infinitely many sign changes for the function

$\pi_{4,1}(x) - \pi_{4,3}(x), \,$

so the lead in the race switches back and forth infinitely many times. The phenomenon that π_4,3(x) is ahead most of the time is called Chebyshev's bias. The prime number race generalizes to other moduli and is the subject of much research; Granville and Martin give a thorough exposition and survey.^[17]

Bounds on the prime-counting function

The prime number theorem is an asymptotic result. Hence, it cannot be used to bound π(x).

However, some bounds on π(x) are known, for instance Pierre Dusart's

$\frac{x}{\ln x}\left(1%2B\frac{1}{\ln x}\right) < \pi(x) < \frac{x}{\ln x}\left(1%2B\frac{1}{\ln x}%2B\frac{2.51}{(\ln x)^2}\right).$

The first inequality holds for all x ≥ 599 and the second one for x ≥ 355991.^[18]

A weaker but sometimes useful bound is

$\frac {x}{\ln x %2B 2} < \pi(x) < \frac {x}{\ln x - 4}$

for x ≥ 55.^[19] In Dusart's thesis there are stronger versions of this type of inequality that are valid for larger x.

The proof by de la Vallée-Poussin implies the following. For every ε > 0, there is an S such that for all x > S,

$\frac {x}{\ln x - (1-\varepsilon)} < \pi(x) < \frac {x}{\ln x - (1%2B\varepsilon)}.$

Approximations for the nth prime number

As a consequence of the prime number theorem, one gets an asymptotic expression for the nth prime number, denoted by p_n:

$p_n \sim n \ln n.$

A better approximation is

${ p_n = n \ln n %2B n \ln \ln n - n %2B \frac{n}{\ln n} \left(\ln \ln n - 2 \right) - \frac{n\ln\ln n}{2(\ln n)^2}\left(\ln\ln n-6\right) %2B O\left( \frac {n} {(\ln n)^2}\right).}$ ^[20]

Rosser's theorem states that p_n is larger than n ln n. This can be improved by the following pair of bounds:^[21]^[22]

$n \ln n %2B n(\ln\ln n - 1) < p_n < n \ln n %2B n \ln \ln n \quad\text{for } n \ge 6.$

Table of π(x), x / ln x, and li(x)

The table compares exact values of π(x) to the two approximations x / ln x and li(x). The last column, x / π(x), is the average prime gap below x.

x	π(x)	π(x) − x / ln x	π(x) / (x / ln x)	li(x) − π(x)	x / π(x)
10	4	−0.3	0.921	2.2	2.500
10²	25	3.3	1.151	5.1	4.000
10³	168	23	1.161	10	5.952
10⁴	1,229	143	1.132	17	8.137
10⁵	9,592	906	1.104	38	10.425
10⁶	78,498	6,116	1.084	130	12.740
10⁷	664,579	44,158	1.071	339	15.047
10⁸	5,761,455	332,774	1.061	754	17.357
10⁹	50,847,534	2,592,592	1.054	1,701	19.667
10¹⁰	455,052,511	20,758,029	1.048	3,104	21.975
10¹¹	4,118,054,813	169,923,159	1.043	11,588	24.283
10¹²	37,607,912,018	1,416,705,193	1.039	38,263	26.590
10¹³	346,065,536,839	11,992,858,452	1.034	108,971	28.896
10¹⁴	3,204,941,750,802	102,838,308,636	1.033	314,890	31.202
10¹⁵	29,844,570,422,669	891,604,962,452	1.031	1,052,619	33.507
10¹⁶	279,238,341,033,925	7,804,289,844,393	1.029	3,214,632	35.812
10¹⁷	2,623,557,157,654,233	68,883,734,693,281	1.027	7,956,589	38.116
10¹⁸	24,739,954,287,740,860	612,483,070,893,536	1.025	21,949,555	40.420
10¹⁹	234,057,667,276,344,607	5,481,624,169,369,960	1.024	99,877,775	42.725
10²⁰	2,220,819,602,560,918,840	49,347,193,044,659,701	1.023	222,744,644	45.028
10²¹	21,127,269,486,018,731,928	446,579,871,578,168,707	1.022	597,394,254	47.332
10²²	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1.021	1,932,355,208	49.636
10²³	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	1.020	7,250,186,216	51.939
OEIS	A006880	A057835		A057752

Analogue for irreducible polynomials over a finite field

There is an analogue of the prime number theorem that describes the "distribution" of irreducible polynomials over a finite field; the form it takes is strikingly similar to the case of the classical prime number theorem.

To state it precisely, let F = GF(q) be the finite field with q elements, for some fixed q, and let N_n be the number of monic irreducible polynomials over F whose degree is equal to n. That is, we are looking at polynomials with coefficients chosen from F, which cannot be written as products of polynomials of smaller degree. In this setting, these polynomials play the role of the prime numbers, since all other monic polynomials are built up of products of them. One can then prove that

$N_n \sim \frac{q^n}{n}.$

If we make the substitution x = qⁿ, then the right hand side is just

$\frac{x}{\log_q x},$

which makes the analogy clearer. Since there are precisely qⁿ monic polynomials of degree n (including the reducible ones), this can be rephrased as follows: if a monic polynomial of degree n is selected randomly, then the probability of it being irreducible is about 1/n.

One can even prove an analogue of the Riemann hypothesis, namely that

$N_n = \frac{q^n}n %2B O\left(\frac{q^{n/2}}{n}\right).$

The proofs of these statements are far simpler than in the classical case. It involves a short combinatorial argument, summarised as follows. Every element of the degree n extension of F is a root of some irreducible polynomial whose degree d divides n; by counting these roots in two different ways one establishes that

$q^n = \sum_{d\mid n} d N_d,$

where the sum is over all divisors d of n. Möbius inversion then yields

$N_n = \frac1n \sum_{d\mid n} \mu(n/d) q^d,$

where μ(k) is the Möbius function. (This formula was known to Gauss.) The main term occurs for d = n, and it is not difficult to bound the remaining terms. The "Riemann hypothesis" statement depends on the fact that the largest proper divisor of n can be no larger than n/2.

Notes

^ Hoffman, Paul (1998). The Man Who Loved Only Numbers. Hyperion. p. 227. ISBN 0-7868-8406-1.
^ N. Costa Pereira (August–September 1985). "A Short Proof of Chebyshev's Theorem". American Mathematical Monthly 92 (7): 494–495. doi:10.2307/2322510. JSTOR 2322510.
^ M. Nair (February 1982). "On Chebyshev-Type Inequalities for Primes". American Mathematical Monthly 89 (2): 126–129. doi:10.2307/2320934. JSTOR 2320934.
^ Ingham, A.E. (1990). The Distribution of Prime Numbers. Cambridge University Press. pp. 2–5. ISBN 0-521-39789-8.
^ D. J. Newman (1980). "Simple analytic proof of the prime number theorem". American Mathematical Monthly 87 (9): 693–696. doi:10.2307/2321853. JSTOR 2321853.
^ D. Zagier (1997). "Newman's short proof of the prime number theorem". American Mathematical Monthly 104 (8): 705–708. doi:10.2307/2975232. JSTOR 2975232. http://mathdl.maa.org/images/upload_library/22/Chauvenet/Zagier.pdf.
^ Video and slides of Tao's lecture on primes, UCLA January 2007.
^ Edwards, Harold M. (2001). Riemann's zeta function. Courier Dover Publications. ISBN 0-4864-1740-9.
^ Helge von Koch (December 1901). "Sur la distribution des nombres premiers". Acta Mathematica 24 (1): 159–182. doi:10.1007/BF02403071. (French)
^ Schoenfeld, Lowell (1976). "Sharper Bounds for the Chebyshev Functions θ(x) and ψ(x). II". Mathematics of Computation 30 (134): 337–360. doi:10.2307/2005976. JSTOR 2005976. .
^ ^a ^b ^c D. Goldfeld The elementary proof of the prime number theorem: an historical perspective.
^ Baas, Nils A.; Skau, Christian F. (2008). "The lord of the numbers, Atle Selberg. On his life and mathematics". Bull. Amer. Math. Soc. 45 (4): 617–649. doi:10.1090/S0273-0979-08-01223-8. http://www.ams.org/bull/2008-45-04/S0273-0979-08-01223-8/S0273-0979-08-01223-8.pdf
^ Cornaros, Charalambos; Dimitracopoulos, Costas (1994). "The prime number theorem and fragments of PA". Archive for Mathematical Logic 33 (4): 265–281. doi:10.1007/BF01270626. http://mpla.math.uoa.gr/~cdimitr/files/publications/AML_33.pdf.
^ Jeremy Avigad, Kevin Donnelly, David Gray, Paul Raff (2005). "A formally verified proof of the prime number theorem". arXiv:cs.AI/0509025 [cs.AI].
^ "Formalizing an analytic proof of the Prime Number Theorem". Journal of Automated Reasoning. 2009, volume = 43, pages = 243––261. http://www.cl.cam.ac.uk/~jrh13/papers/mikefest.html.
^ Ivan Soprounov (1998). A short proof of the Prime Number Theorem for arithmetic progressions. http://www.math.umass.edu/~isoprou/pdf/primes.pdf.
^ ^a ^b ^c Granville, Andrew; Martin, Greg (January 2006). "Prime Number Races". American Mathematical Monthly 113 (1): 1–33. doi:10.2307/27641834. JSTOR 27641834. http://www.dms.umontreal.ca/%7Eandrew/PDF/PrimeRace.pdf.
^ Dusart, Pierre (1998). Autour de la fonction qui compte le nombre de nombres premiers. http://www.unilim.fr/laco/theses/1998/T1998_01.html. (French)
^ Barkley Rosser (January 1941). "Explicit Bounds for Some Functions of Prime Numbers". American Journal of Mathematics 63 (1): 211–232. doi:10.2307/2371291. JSTOR 2371291.
^ Ernest Cesàro (1894). "Sur une formule empirique de M. Pervouchine". Comptes rendus hebdomadaires des séances de l'Académie des sciences 119: 848–849. http://gallica.bnf.fr/ark:/12148/bpt6k30752. (French)
^ Eric Bach, Jeffrey Shallit (1996). Algorithmic Number Theory. 1. MIT Press. p. 233. ISBN 0-262-02405-5.
^ Pierre Dusart (1999). "The kth prime is greater than k(ln k + ln ln k−1) for k ≥ 2". Mathematics of Computation 68: 411–415. http://www.ams.org/mcom/1999-68-225/S0025-5718-99-01037-6/S0025-5718-99-01037-6.pdf.

References

Hardy, G. H. & Littlewood, J. E. (1916). "Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes". Acta Mathematica 41: 119–196. doi:10.1007/BF02422942.
Granville, Andrew (1995). "Harald Cramér and the distribution of prime numbers". Scandinavian Actuarial Journal 1: 12–28. http://www.dartmouth.edu/~chance/chance_news/for_chance_news/Riemann/cramer.pdf.

External links

Table of Primes by Anton Felkel.
Prime formulas and Prime number theorem at MathWorld.
Prime number theorem on PlanetMath
How Many Primes Are There? and The Gaps between Primes by Chris Caldwell, University of Tennessee at Martin.
Tables of prime-counting functions by Tomás Oliveira e Silva