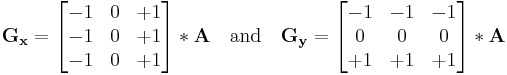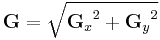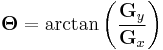Prewitt operator

Feature detection
Output of a typical corner detection algorithm
Edge detection
Canny · Canny-Deriche · Differential · Sobel · Prewitt · Roberts Cross
Interest point detection
Corner detection
Harris operator · Shi and Tomasi · Level curve curvature · SUSAN · FAST
Blob detection
Laplacian of Gaussian (LoG) · Difference of Gaussians (DoG) · Determinant of Hessian (DoH) · Maximally stable extremal regions · PCBR
Ridge detection
Hough transform
Structure tensor
Affine invariant feature detection
Affine shape adaptation · Harris affine · Hessian affine
Feature description
SIFT · SURF · GLOH · HOG · LESH
Scale-space
Scale-space axioms · Implementation details · Pyramids

The Prewitt operator is used in image processing, particularly within edge detection algorithms. Technically, it is a discrete differentiation operator, computing an approximation of the gradient of the image intensity function. At each point in the image, the result of the Prewitt operator is either the corresponding gradient vector or the norm of this vector. The Prewitt operator is based on convolving the image with a small, separable, and integer valued filter in horizontal and vertical direction and is therefore relatively inexpensive in terms of computations. On the other hand, the gradient approximation which it produces is relatively crude, in particular for high frequency variations in the image.

Contents

Simplified description

In simple terms, the operator calculates the gradient of the image intensity at each point, giving the direction of the largest possible increase from light to dark and the rate of change in that direction. The result therefore shows how "abruptly" or "smoothly" the image changes at that point, and therefore how likely it is that that part of the image represents an edge, as well as how that edge is likely to be oriented. In practice, the magnitude (likelihood of an edge) calculation is more reliable and easier to interpret than the direction calculation.

Mathematically, the gradient of a two-variable function (here the image intensity function) is at each image point a 2D vector with the components given by the derivatives in the horizontal and vertical directions. At each image point, the gradient vector points in the direction of largest possible intensity increase, and the length of the gradient vector corresponds to the rate of change in that direction. This implies that the result of the Prewitt operator at an image point which is in a region of constant image intensity is a zero vector and at a point on an edge is a vector which points across the edge, from darker to brighter values.

Formulation

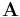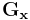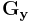Mathematically, the operator uses two 3×3 kernels which are convolved with the original image to calculate approximations of the derivatives - one for horizontal changes, and one for vertical. If we define \mathbf{A} as the source image, and \mathbf{G_x} and \mathbf{G_y} are two images which at each point contain the horizontal and vertical derivative approximations, the latter are computed as:

\mathbf{G_x} = \begin{bmatrix} -1 & 0 & %2B1 \\ -1 & 0 & %2B1 \\ -1 & 0 & %2B1 \end{bmatrix} * \mathbf{A} \quad \mbox{and} \quad \mathbf{G_y} = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ %2B1 & %2B1 & %2B1 \end{bmatrix} * \mathbf{A}

where * here denotes the 2-dimensional convolution operation.

The x-coordinate is here defined as increasing in the "right"-direction, and the y-coordinate is defined as increasing in the "down"-direction. At each point in the image, the resulting gradient approximations can be combined to give the gradient magnitude, using:

\mathbf{G} = \sqrt{ {\mathbf{G}_x}^2 %2B {\mathbf{G}_y}^2 }

Using this information, we can also calculate the gradient's direction:

\mathbf{\Theta} = \operatorname{arctan}\left({ \mathbf{G}_y \over \mathbf{G}_x }\right)

where, for example, Θ is 0 for a vertical edge which is darker on the right side.

Example

See also

References