Pretzel link
In knot theory, a branch of mathematics, a pretzel link is a special kind of link. A pretzel link which is also a knot (i.e. a link with one component) is a pretzel knot.
In the standard projection of the 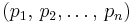 pretzel link, there are
pretzel link, there are 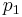 left-handed crossings in the first tangle,
left-handed crossings in the first tangle, 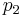 in the second, and, in general,
in the second, and, in general, 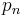 in the nth.
in the nth.
A pretzel link can also be described as a Montesinos link with integer tangles.
Contents |
Some basic results
The 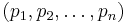 pretzel link is a knot iff both
pretzel link is a knot iff both  and all the
and all the 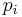 are odd or exactly one of the
are odd or exactly one of the 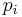 is even.[1]
is even.[1]
The 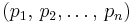 pretzel link is split if at least two of the
pretzel link is split if at least two of the 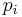 are zero; but the converse is false.
are zero; but the converse is false.
The 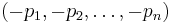 pretzel link is the mirror image of the
pretzel link is the mirror image of the 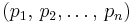 pretzel link.
pretzel link.
The 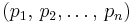 pretzel link is link-equivalent (i.e. homotopy-equivalent in S3) to the
pretzel link is link-equivalent (i.e. homotopy-equivalent in S3) to the  pretzel link. Thus, too, the
pretzel link. Thus, too, the 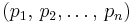 pretzel link is link-equivalent to the
pretzel link is link-equivalent to the 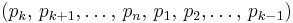 pretzel link.[1]
pretzel link.[1]
The 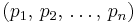 pretzel link is link-equivalent to the
pretzel link is link-equivalent to the 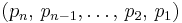 pretzel link. However, if one orients the links in a canonical way, then these two links have opposite orientations.
pretzel link. However, if one orients the links in a canonical way, then these two links have opposite orientations.
Some examples
The (−1, −1, −1) pretzel knot is the trefoil; the (0, 3, −1) pretzel knot is its mirror image.
The (5, −1, −1) pretzel knot is the stevedore knot (61).
If p, q, r are distinct odd integers greater than 1, then the (p, q, r) pretzel knot is a non-invertible knot.
The (2p,\ 2q, 2r) pretzel link is a link formed by three linked unknots.
The (−3, 0, −3) pretzel knot is the connected sum of two trefoil knots.
The (0, q, 0) pretzel link is the split union of an unknot and another knot.
Utility
(−2, 3, 2n + 1) pretzel links are especially useful in the study of 3-manifolds. Many results have been stated about the manifolds that result from Dehn surgery on the (−2,3,7) pretzel knot in particular.
Pretzel knots can be used to introduce students to the essentials of knot theory by making edible pretzels.
References
- Trotter, Hale F.: Non-invertible knots exist, Topology, 2 (1963), 272–280.