Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.
For example, all partial orders and equivalence relations are preorders. The name quasi-order is also common for preorders.
Many order theoretical definitions for partially ordered sets can be generalized to preorders, but the extra effort of generalization is rarely needed.
Contents |
Formal definition
Consider some set P and a binary relation ≤ on P. Then ≤ is a preorder, or quasiorder, if it is reflexive and transitive, i.e., for all a, b and c in P, we have that:
- a ≤ a (reflexivity)
- if a ≤ b and b ≤ c then a ≤ c (transitivity)
Note that an alternate definition of preorder requires the relation to be irreflexive. However, as this article is examining preorders as a logical extension of partial orders, the current definition is more intuitive.
A set that is equipped with a preorder is called a preordered set.
If a preorder is also antisymmetric, that is, a ≤ b and b ≤ a implies a = b, then it is a partial order.
On the other hand, if it is symmetric, that is, if a ≤ b implies b ≤ a, then it is an equivalence relation.
A preorder which is preserved in all contexts (i.e. respected by all functions on P) is called a precongruence. A precongruence which is also symmetric (i.e. is an equivalence relation) is a congruence relation.
Equivalently, a preorder on the set P can be defined as a category with object set P where every homset has at most one element (one for objects which are related, zero otherwise).
Examples of preorders
- Any collection of sets is preordered by their comparative sizes. Thus {3, 7} ≤ {April, June, July}. This applies equally to infinite sets; as one example, Cantor's famous diagonalization result that the real numbers are uncountable (i.e., more numerous than the integers) may be expressed in terms of this preorder as Z < R.
- Logical implication over sentences.
- Every finite topological space gives rise to a preorder on its points, in which x ≤ y if and only if x belongs to every neighborhood of y, and every finite preorder can be formed as the specialization preorder of a topological space in this way. That is, there is a 1-to-1 correspondence between finite topologies and finite preorders. However, the relation between infinite topological spaces and their specialization preorders is not 1-to-1.
- A net is a directed preorder, that is, each pair of elements has an upper bound. The definition of convergence via nets is important in topology, where preorders cannot be replaced by partially ordered sets without losing important features.
- The relation defined by
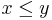 iff
iff 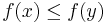 , where f is a function into some preorder.
, where f is a function into some preorder. - The relation defined by
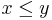 iff there exists some injection from x to y. Injection may be replaced by surjection, or any type of structure-preserving function, such as ring homomorphism, or permutation.
iff there exists some injection from x to y. Injection may be replaced by surjection, or any type of structure-preserving function, such as ring homomorphism, or permutation. - The embedding relation for countable total orderings.
- The graph-minor relation in graph theory.
In computer science, one can find examples of the following preorders.
- The subtyping relations are usually preorders.
- Simulation preorders are preorders (hence the name).
Example of a total preorder:
- Preference, according to common models.
Constructions
Every binary relation R on a set S can be extended to a preorder on S by taking the transitive closure and reflexive closure, R+=. The transitive closure indicates path connection in R: x R+ y if and only if there is an R-path from x to y.
Given a preorder  on S one may define an equivalence relation ~ on S such that a ~ b if and only if a
on S one may define an equivalence relation ~ on S such that a ~ b if and only if a  b and b
b and b  a. (The resulting relation is reflexive since a preorder is reflexive, transitive by applying transitivity of the preorder twice, and symmetric by definition.)
a. (The resulting relation is reflexive since a preorder is reflexive, transitive by applying transitivity of the preorder twice, and symmetric by definition.)
Using this relation, it is possible to construct a partial order on the quotient set of the equivalence, S / ~, the set of all equivalence classes of ~. Note that if the preorder is R+=, S / ~ is the set of R-cycle equivalence classes: x ∈ [y] if and only if x = y or x is in an R-cycle with y. In any case, on S / ~ we can define [x] ≤ [y] if and only if x  y. By the construction of ~ , this definition is independent of the chosen representatives and the corresponding relation is indeed well-defined. It is readily verified that this yields a partially ordered set.
y. By the construction of ~ , this definition is independent of the chosen representatives and the corresponding relation is indeed well-defined. It is readily verified that this yields a partially ordered set.
Conversely, from a partial order on a partition of a set S one can construct a preorder on S. There is a 1-to-1 correspondence between preorders and pairs (partition, partial order).
For a preorder " ", a relation "<" can be defined as a < b if and only if (a
", a relation "<" can be defined as a < b if and only if (a  b and not b
b and not b  a), or equivalently, using the equivalence relation introduced above, (a
a), or equivalently, using the equivalence relation introduced above, (a  b and not a ~ b). It is a strict partial order; every strict partial order can be the result of such a construction. If the preorder is anti-symmetric, hence a partial order "≤", the equivalence is equality, so the relation "<" can also be defined as a < b if and only if (a ≤ b and a ≠ b).
b and not a ~ b). It is a strict partial order; every strict partial order can be the result of such a construction. If the preorder is anti-symmetric, hence a partial order "≤", the equivalence is equality, so the relation "<" can also be defined as a < b if and only if (a ≤ b and a ≠ b).
(Alternatively, for a preorder " ", a relation "<" can be defined as a < b if and only if (a
", a relation "<" can be defined as a < b if and only if (a  b and a ≠ b). The result is the reflexive reduction of the preorder. However, if the preorder is not anti-symmetric the result is not transitive, and if it is, as we have seen, it is the same as before.)
b and a ≠ b). The result is the reflexive reduction of the preorder. However, if the preorder is not anti-symmetric the result is not transitive, and if it is, as we have seen, it is the same as before.)
Conversely we have a  b if and only if a < b or a ~ b. This is the reason for using the notation "
b if and only if a < b or a ~ b. This is the reason for using the notation " "; "≤" can be confusing for a preorder that is not anti-symmetric, it may suggest that a ≤ b implies that a < b or a = b.
"; "≤" can be confusing for a preorder that is not anti-symmetric, it may suggest that a ≤ b implies that a < b or a = b.
Note that with this construction multiple preorders " " can give the same relation "<", so without more information, such as the equivalence relation, "
" can give the same relation "<", so without more information, such as the equivalence relation, " " cannot be reconstructed from "<". Possible preorders include the following:
" cannot be reconstructed from "<". Possible preorders include the following:
- Define a ≤ b as a < b or a = b (i.e., take the reflexive closure of the relation). This gives the partial order associated with the strict partial order "<" through reflexive closure; in this case the equivalence is equality, so we don't need the notations
 and ~.
and ~. - Define a
 b as "not b < a" (i.e., take the inverse complement of the relation), which corresponds to defining a ~ b as "neither a < b nor b < a"; these relations
b as "not b < a" (i.e., take the inverse complement of the relation), which corresponds to defining a ~ b as "neither a < b nor b < a"; these relations  and ~ are in general not transitive; however, if they are, ~ is an equivalence; in that case "<" is a strict weak order. The resulting preorder is total.
and ~ are in general not transitive; however, if they are, ~ is an equivalence; in that case "<" is a strict weak order. The resulting preorder is total.
Number of preorders
| Number of n-element binary relations of different types | ||||||||
|---|---|---|---|---|---|---|---|---|
| n | all | transitive | reflexive | preorder | partial order | total preorder | total order | equivalence relation |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65536 | 3994 | 4096 | 355 | 219 | 75 | 24 | 15 |
| OEIS | A002416 | A006905 | A053763 | A000798 | A001035 | A000670 | A000142 | A000110 |
As explained above, there is a 1-to-1 correspondence between preorders and pairs (partition, partial order). Thus the number of preorders is the sum of the number of partial orders on every partition. For example:
- for n=3:
- 1 partition of 3, giving 1 preorder
- 3 partitions of 2+1, giving 3 × 3 = 9 preorders
- 1 partition of 1+1+1, giving 19 preorders
- i.e. together 29 preorders.
- for n=4:
- 1 partition of 4, giving 1 preorder
- 7 partitions with two classes (4 of 3+1 and 3 of 2+2), giving 7 × 3 = 21 preorders
- 6 partitions of 2+1+1, giving 6 × 19 = 114 preorders
- 1 partition of 1+1+1+1, giving 219 preorders
- i.e. together 355 preorders.
Interval
For a  b, the interval [a,b] is the set of points x satisfying a
b, the interval [a,b] is the set of points x satisfying a  x and x
x and x  b, also written a
b, also written a  x
x  b. It contains at least the points a and b. One may choose to extend the definition to all pairs (a,b). The extra intervals are all empty.
b. It contains at least the points a and b. One may choose to extend the definition to all pairs (a,b). The extra intervals are all empty.
Using the corresponding strict relation "<", one can also define the interval (a,b) as the set of points x satisfying a < x and x < b, also written a < x < b. An open interval may be empty even if a < b.
Also [a,b) and (a,b] can be defined similarly.
See also
- partial order - preorder that is antisymmetric
- equivalence relation - preorder that is symmetric
- total preorder - preorder that is total
- total order - preorder that is antisymmetric and total
- directed set
- category of preordered sets
- prewellordering
- preordered class
- Well-quasi-ordering
References
- Schröder, Bernd S. W. (2002), Ordered Sets: An Introduction, Boston: Birkhäuser, ISBN 0-8176-4128-9