Potential evaporation
Potential evaporation or potential evapotranspiration (PET) is defined as the amount of evaporation that would occur if a sufficient water source were available. If the actual evapotranspiration is considered the net result of atmospheric demand for moisture from a surface and the ability of the surface to supply moisture, then PET is a measure of the demand side. Surface and air temperatures, insolation, and wind all affect this. A dryland is a place where annual potential evaporation exceeds annual precipitation.
Contents |
Estimates of potential evaporation (mm)
Thornthwaite equation (1948)

Where
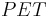 is the estimated potential evapotranspiration (cm/month)
is the estimated potential evapotranspiration (cm/month)
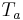 is the average daily temperature (degrees Celsius; if this is negative, use
is the average daily temperature (degrees Celsius; if this is negative, use 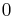 ) of the month being calculated
) of the month being calculated
 is the number of days in the month being calculated
is the number of days in the month being calculated
 is the average day length (hours) of the month being calculated
is the average day length (hours) of the month being calculated

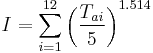 is a heat index which depends on the 12 monthly mean temperatures
is a heat index which depends on the 12 monthly mean temperatures  .[1]
.[1]
Somewhat modified forms of this equation appear in later publications (1955 and 1957) by Thornthwaite and Mather. [2]
Penman equation (1948)
Penman-Monteith equation (1965)
See also
References
- ^ Thornthwaite, C. W. (1948). "An approach toward a rational classification of climate". Geographical Review 38 (1): 55–94. doi:10.2307/210739. http://www.unc.edu/courses/2007fall/geog/801/001/www/ET/Thornthwaite48-GeogrRev.pdf
- ^ Black, Peter E. (2007). "Revisiting the Thornthwaite and Mather water balance". Journal of the American Water Resources Association 43 (6): 1604–1605. doi:10.1111/j.1752-1688.2007.00132.x. http://www.watershedhydrology.com/pdf/T&M%20Revisited.pdf
- Penman, H.L. (1948). "Natural evaporation from open water, bare soil, and grass". Proc. Roy. Soc. (London, U.K.) A193 (1032): 120–145. Bibcode 1948RSPSA.193..120P. doi:10.1098/rspa.1948.0037.
- Brutsaert, W.H. (1982). Evaporation into the Atmosphere: theory, history, and applications. Dortrecht, Holland: D. Reidel. ISBN 9027712476.
- Bonan, Gordon (2002). Ecological Climatology. Cambridge, U.K.: CUP. ISBN 978-0-521-80476-0.
External links
- ag.arizona.edu Global map of potential evaporation.