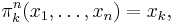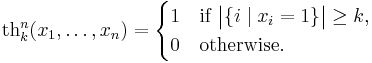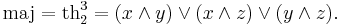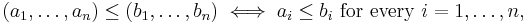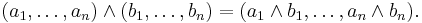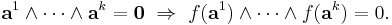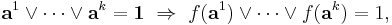Post's lattice
In logic and universal algebra, Post's lattice denotes the lattice of all clones on a two-element set {0, 1}, ordered by inclusion. It is named for Emil Post, who published a complete description of the lattice in 1941.[1] The relative simplicity of Post's lattice is in stark contrast to the lattice of clones on a three-element (or larger) set, which has the cardinality of the continuum, and a complicated inner structure. A modern exposition of Post's result can be found in Lau (2006).[2]
Contents |
Basic concepts
A Boolean function, or logical connective, is an n-ary operation f: 2n → 2 for some n ≥ 1, where 2 denotes the two-element set {0, 1}. Particular Boolean functions are the projections
and given an m-ary function f, and n-ary functions g1, ..., gm, we can construct another n-ary function
called their composition. A set of functions closed under composition, and containing all projections, is called a clone.
Let B be a set of connectives. The functions which can be defined by a formula using propositional variables and connectives from B form a clone [B], indeed it is the smallest clone which includes B. We call [B] the clone generated by B, and say that B is the basis of [B]. For example, [¬, ⋀] are all Boolean functions, and [0, 1, ⋀, ⋁] are the monotone functions.
We use the operations ¬ (negation), ⋀ (conjunction or meet), ⋁ (disjunction or join), → (implication), ↔ (biconditional), + (exclusive disjunction or Boolean ring addition), ↛ (nonimplication), ?: (the ternary conditional operator) and the constant unary functions 0 and 1. Moreover, we need the threshold functions
For example, th1n is the large disjunction of all the variables xi, and thnn is the large conjunction. Of particular importance is the majority function
We denote elements of 2n (i.e., truth-assignments) as vectors: a = (a1, ..., an). The set 2n carries a natural product Boolean algebra structure. That is, ordering, meets, joins, and other operations on n-ary truth assignments are defined pointwise:
Naming of clones
Intersection of an arbitrary number of clones is again a clone. It is convenient to denote intersection of clones by simple juxtaposition, i.e., the clone C1 ⋂ C2 ⋂ ... ⋂ Ck is denoted by C1C2...Ck. Some special clones are introduced below:
- M is the set of monotone functions: f(a) ≤ f(b) for every a ≤ b.
- D is the set of self-dual functions: ¬f(a) = f(¬a).
- A is the set of affine functions: the functions satisfying
-
- for every i ≤ n, a, b ∈ 2n, and c, d ∈ 2. Equivalently, the functions expressible as f(x1, ..., xn) = a0 + a1x1 + ... + anxn for some a0, a.
- U is the set of essentially unary functions, i.e., functions which depend on at most one input variable: there exists an i = 1, ..., n such that f(a) = f(b) whenever ai = bi.
- Λ is the set of conjunctive functions: f(a ⋀ b) = f(a) ⋀ f(b). The clone Λ consists of the conjunctions
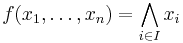 for all subsets I of {1, ..., n} (including the empty conjunction, i.e., the constant 1), and the constant 0.
for all subsets I of {1, ..., n} (including the empty conjunction, i.e., the constant 1), and the constant 0. - V is the set of disjunctive functions: f(a ⋁ b) = f(a) ⋁ f(b). Equivalently, V consists of the disjunctions
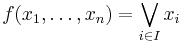 for all subsets I of {1, ..., n} (including the empty disjunction 0), and the constant 1.
for all subsets I of {1, ..., n} (including the empty disjunction 0), and the constant 1. - For any k ≥ 1, T0k is the set of functions f such that
-
- Moreover,
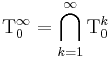 is the set of functions bounded above by a variable: there exists i = 1, ..., n such that f(a) ≤ ai for all a.
is the set of functions bounded above by a variable: there exists i = 1, ..., n such that f(a) ≤ ai for all a. - As a special case, P0 = T01 is the set of 0-preserving functions: f(0) = 0.
- For any k ≥ 1, T1k is the set of functions f such that
-
- and
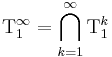 is the set of functions bounded below by a variable: there exists i = 1, ..., n such that f(a) ≥ ai for all a.
is the set of functions bounded below by a variable: there exists i = 1, ..., n such that f(a) ≥ ai for all a. - The special case P1 = T11 consists of the 1-preserving functions: f(1) = 1.
- The largest clone of all functions is denoted ⊤, the smallest clone (which contains only projections) is denoted ⊥, and P = P0P1 is the clone of constant-preserving functions.
Lattice
The set of all clones is a closure system, hence it forms a complete lattice. The lattice is countably infinite, and all its members are finitely generated. All the clones are listed in the table below.
| clone | one of its bases |
|---|---|
| ⊤ | ⋁, ¬ |
| P0 | ⋁, + |
| P1 | ⋀, → |
| P | ?: |
| T0k, k ≥ 2 | thkk+1, ↛ |
| T0∞ | ↛ |
| PT0k, k ≥ 2 | thkk+1, x ⋀ (y → z) |
| PT0∞ | x ⋀ (y → z) |
| T1k, k ≥ 2 | th2k+1, → |
| T1∞ | → |
| PT1k, k ≥ 2 | th2k+1, x ⋁ (y + z) |
| PT1∞ | x ⋁ (y + z) |
| M | ⋀, ⋁, 0, 1 |
| MP0 | ⋀, ⋁, 0 |
| MP1 | ⋀, ⋁, 1 |
| MP | ⋀, ⋁ |
| MT0k, k ≥ 2 | thkk+1, 0 |
| MT0∞ | x ⋀ (y ⋁ z), 0 |
| MPT0k, k ≥ 2 | thkk+1 for k ≥ 3, maj, x ⋀ (y ⋁ z) for k = 2 |
| MPT0∞ | x ⋀ (y ⋁ z) |
| MT1k, k ≥ 2 | th2k+1, 1 |
| MT1∞ | x ⋁ (y ⋀ z), 1 |
| MPT1k, k ≥ 2 | th2k+1 for k ≥ 3, maj, x ⋁ (y ⋀ z) for k = 2 |
| MPT1∞ | x ⋁ (y ⋀ z) |
| Λ | ⋀, 0, 1 |
| ΛP0 | ⋀, 0 |
| ΛP1 | ⋀, 1 |
| ΛP | ⋀ |
| V | ⋁, 0, 1 |
| VP0 | ⋁, 0 |
| VP1 | ⋁, 1 |
| VP | ⋁ |
| D | maj, ¬ |
| DP | maj, x + y + z |
| DM | maj |
| A | ↔, 0 |
| AD | ¬, x + y + z |
| AP0 | + |
| AP1 | ↔ |
| AP | x + y + z |
| U | ¬, 0 |
| UD | ¬ |
| UM | 0, 1 |
| UP0 | 0 |
| UP1 | 1 |
| ⊥ |
The eight infinite families have actually also members with k = 1, but these appear separately in the table: T01 = P0, T11 = P1, PT01 = PT11 = P, MT01 = MP0, MT11 = MP1, MPT01 = MPT11 = MP.
The lattice has a natural symmetry mapping each clone C to its dual clone Cd = {fd | f ∈ C}, where fd(x1, ..., xn) = ¬f(¬x1, ..., ¬xn) is the de Morgan dual of a Boolean function f. For example, Λd = V, (T0k)d = T1k, and Md = M.
Applications
The complete classification of Boolean clones given by Post helps to resolve various questions about classes of Boolean functions. For example:
- An inspection of the lattice shows that the maximal clones different from ⊤ (often called Post's classes) are M, D, A, P0, P1, and every proper subclone of ⊤ is contained in one of them. As a set B of connectives is functionally complete if and only if it generates ⊤, we obtain the following characterization: B is functionally complete iff it is not included in one of the five Post's classes.
- The satisfiability problem for Boolean formulas is NP-complete by Cook's theorem. Consider a restricted version of the problem: for a fixed finite set B of connectives, let B-SAT be the algorithmic problem of checking whether a given B-formula is satisfiable. Lewis[3] used the description of Post's lattice to show that B-SAT is NP-complete if the function ↛ can be generated from B (i.e., [B] ⊇ T0∞), and in all the other cases B-SAT is polynomial-time decidable.
Variants
Post originally did not work with the modern definition of clones, but with the so-called iterative systems, which are sets of operations closed under substitution
as well as permutation and identification of variables. The main difference is that iterative systems do not necessarily contain all projections. Every clone is an iterative system, and there are 20 non-empty iterative systems which are not clones. (Post also excluded the empty iterative system from the classification, hence his diagram has no least element and fails to be a lattice.) As another alternative, some authors work with the notion of a closed class, which is an iterative system closed under introduction of dummy variables. There are four closed classes which are not clones: the empty set, the set of constant 0 functions, the set of constant 1 functions, and the set of all constant functions.
Composition alone does not allow to generate a nullary function from the corresponding unary constant function, this is the technical reason why nullary functions are excluded from clones in Post's classification. If we lift the restriction, we get more clones. Namely, each clone C in Post's lattice which contains at least one constant function corresponds to two clones under the less restrictive definition: C, and C together with all nullary functions whose unary versions are in C.
References
- ^ E. L. Post, The two-valued iterative systems of mathematical logic, Annals of Mathematics studies, no. 5, Princeton University Press, Princeton 1941, 122 pp.
- ^ D. Lau, Function algebras on finite sets: Basic course on many-valued logic and clone theory, Springer, New York, 2006, 668 pp. ISBN 978-3-540-36022-3
- ^ H. R. Lewis, Satisfiability problems for propositional calculi, Mathematical Systems Theory 13 (1979), pp. 45–53.