Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four. It applies to real vector bundles.
Contents |
Definition
Given a real vector bundle E over M, its k-th Pontryagin class 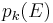 is defined as
is defined as
Here 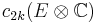 denotes the 2k-th Chern class of the complexification
denotes the 2k-th Chern class of the complexification 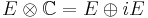 of E and
of E and 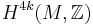 , the 4k-cohomology group of
, the 4k-cohomology group of  with integer coefficients.
with integer coefficients.
The rational Pontryagin class 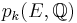 is defined to be the image of
is defined to be the image of 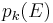 in
in 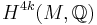 , the 4k-cohomology group of
, the 4k-cohomology group of  with rational coefficients.
with rational coefficients.
Properties
The total Pontryagin class
is (modulo 2-torsion) multiplicative with respect to Whitney sum of vector bundles, i.e.,
for two vector bundles E and F over M. In terms of the individual Pontryagin classes 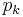 ,
,
and so on.
The vanishing of the Pontryagin classes and Stiefel-Whitney classes of a vector bundle does not guarantee that the vector bundle is trivial. For example, up to vector bundle isomorphism, there is a unique nontrivial rank 10 vector bundle 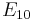 over the 9-sphere. (The clutching function for
over the 9-sphere. (The clutching function for 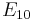 arises from the stable homotopy group
arises from the stable homotopy group 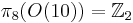 .) The Pontryagin classes and Stiefel-Whitney classes all vanish: the Pontryagin classes don't exist in degree 9, and the Stiefel-Whitney class
.) The Pontryagin classes and Stiefel-Whitney classes all vanish: the Pontryagin classes don't exist in degree 9, and the Stiefel-Whitney class 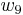 of
of 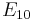 vanishes by the Wu formula
vanishes by the Wu formula 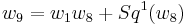 . Moreover, this vector bundle is stably nontrivial, i.e. the Whitney sum of
. Moreover, this vector bundle is stably nontrivial, i.e. the Whitney sum of 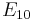 with any trivial bundle remains nontrivial. (Hatcher 2009, p. 76)
with any trivial bundle remains nontrivial. (Hatcher 2009, p. 76)
Given a 2k-dimensional vector bundle E we have
where 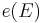 denotes the Euler class of E, and
denotes the Euler class of E, and 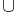 denotes the cup product of cohomology classes; under the splitting principle, this corresponds to the square of the Vandermonde polynomial being the discriminant.
denotes the cup product of cohomology classes; under the splitting principle, this corresponds to the square of the Vandermonde polynomial being the discriminant.
Pontryagin classes and curvature
As was shown by Shiing-Shen Chern and André Weil around 1948, the rational Pontryagin classes
can be presented as differential forms which depend polynomially on the curvature form of a vector bundle. This Chern-Weil theory revealed a major connection between algebraic topology and global differential geometry.
For a vector bundle E over a n-dimensional differentiable manifold M equipped with a connection, the total Pontryagin class is expressed as
where  denotes the curvature form, and
denotes the curvature form, and 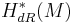 denotes the de Rham cohomology groups.
denotes the de Rham cohomology groups.
Pontryagin classes of a manifold
The Pontryagin classes of a smooth manifold are defined to be the Pontryagin classes of its tangent bundle.
Novikov proved in 1966 that if manifolds are homeomorphic then their rational Pontryagin classes: 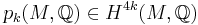 are the same.
are the same.
If the dimension is at least five, there are at most finitely many different smooth manifolds with given homotopy type and Pontryagin classes.
Pontryagin numbers
Pontryagin numbers are certain topological invariants of a smooth manifold. The Pontryagin number vanishes if the dimension of manifold is not divisible by 4. It is defined in terms of the Pontryagin classes of a manifold as follows:
Given a smooth 4n-dimensional manifold M and a collection of natural numbers
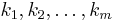 such that
such that 
the Pontryagin number 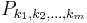 is defined by
is defined by
where 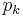 denotes the k-th Pontryagin class and [M] the fundamental class of M.
denotes the k-th Pontryagin class and [M] the fundamental class of M.
Properties
- Pontryagin numbers are oriented cobordism invariant; and together with Stiefel-Whitney numbers they determine an oriented manifold's oriented cobordism class.
- Pontryagin numbers of closed Riemannian manifold (as well as Pontryagin classes) can be calculated as integrals of certain polynomial from curvature tensor of Riemannian manifold.
- Such invariants as signature and
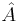 -genus can be expressed through Pontryagin numbers.
-genus can be expressed through Pontryagin numbers.
Generalizations
There is also a quaternionic Pontryagin class, for vector bundles with quaternion structure.
See also
References
- Milnor John W.; Stasheff, James D. (1974). Characteristic classes. Annals of Mathematics Studies, No. 76. Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo. ISBN 0-691-08122-0.
- Hatcher, Allen (2009). Vector Bundles & K-Theory (2.1 ed.). http://www.math.cornell.edu/~hatcher/VBKT/VBpage.html
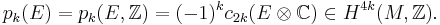
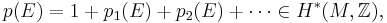
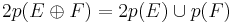
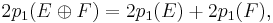
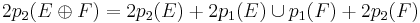
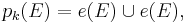
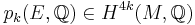
![p=\left[1-\frac{{\rm Tr}(\Omega ^2)}{8 \pi ^2}%2B\frac{{\rm Tr}(\Omega ^2)^2-2 {\rm Tr}(\Omega ^4)}{128 \pi ^4}-\frac{{\rm Tr}(\Omega ^2)^3-6 {\rm Tr}(\Omega ^2) {\rm Tr}(\Omega ^4)%2B8 {\rm Tr}(\Omega ^6)}{3072 \pi ^6}%2B\cdots\right]\in H^*_{dR}(M)](/2012-wikipedia_en_all_nopic_01_2012/I/dc4a92520fd6e27bd460a7385787a1a1.png)
![P_{k_1,k_2,\dots, k_m}=p_{k_1}\cup p_{k_2}\cup \cdots\cup p_{k_m}([M])](/2012-wikipedia_en_all_nopic_01_2012/I/21660a243635a265f7b1aca103950837.png)