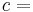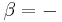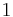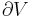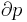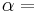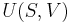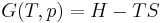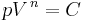Polytropic process

Thermodynamics
Branches Classical · Statistical · Chemical Equilibrium / Non-equilibrium Thermofluids
Laws Zeroth · First · Second · Third
Systems State: Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency
System properties Property diagrams Intensive and extensive properties State functions: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat
Material properties Specific heat capacity  Compressibility  Thermal expansion  Property database
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Table of thermodynamic equations
Potentials Free energy · Free entropy Internal energy Enthalpy Helmholtz free energy Gibbs free energy
History and culture Philosophy: Entropy and time · Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics History: General · Heat · Entropy · Gas laws Perpetual motion Theories: Caloric theory · Vis viva Theory of heat Mechanical equivalent of heat Motive power Publications: "An Experimental Enquiry Concerning ... Heat" "On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines of: Thermodynamics · Heat engines Art: Maxwell's thermodynamic surface Education: Entropy as energy dispersal
Scientists Daniel Bernoulli Sadi Carnot Benoît Paul Émile Clapeyron Rudolf Clausius Hermann von Helmholtz Constantin Carathéodory Pierre Duhem Josiah Willard Gibbs James Prescott Joule James Clerk Maxwell Julius Robert von Mayer William Rankine John Smeaton Georg Ernst Stahl Benjamin Thompson William Thomson, 1st Baron Kelvin John James Waterston

A polytropic process is a thermodynamic process that obeys the relation:

where p is the pressure, V is volume, n, the polytropic index, is any real number, and C is a constant. This equation can be used to accurately characterize processes of certain systems, notably the compression or expansion of a gas and in some cases liquids and solids.

Applicability

The equation is a valid characterization of a thermodynamic process assuming that the process is quasistatic and the values of the heat capacities, 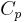and 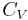, are almost constant when is not zero or infinity. (In reality, 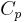and 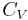are actually functions of temperature and pressure, but are nearly constant within small changes of temperature).

Under standard conditions, most gases can be accurately characterized by the ideal gas law. This construct allows for the pressure-volume relationship to be defined for essentially all ideal thermodynamic cycles, such as the well-known Carnot cycle. Note however that there may also be instances where a polytropic process occurs in a non-ideal gas.

Relationship to ideal processes

For certain values of the polytropic index, the process will be synonymous with other common processes. Some examples of the effects of varying index values are given in the table.

Variation of polytropic index

Polytropic index	Relation	Effects
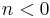	—	An explosion occurs
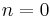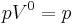	(constant)	Equivalent to an isobaric process (constant pressure)
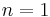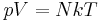	(constant)	Equivalent to an isothermal process (constant temperature)
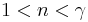	—	A quasi-adiabatic process such as in an internal combustion engine during expansion, or in vapor compression refrigeration during compression
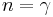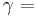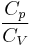	—	is the adiabatic index, yielding an adiabatic process (no heat transferred)
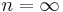	—	Equivalent to an isochoric process (constant volume)

When the index n is between any two of the former values (0, 1, gamma, or infinity), it means that the polytropic curve will bounded by the curves of the two corresponding indices.

Note that 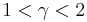, since .

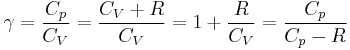Notation

In the case of an isentropic ideal gas, is the ratio of specific heats, known as the adiabatic index or as adiabatic exponent.

An isothermal ideal gas is also a polytropic gas. Here, the polytropic index is equal to one, and differs from the adiabatic index .

In order to discriminate between the two gammas, the polytropic gamma is sometimes capitalized, .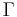

To confuse matters further, some authors refer to 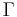as the polytropic index, rather than . Note that

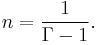
Other

A solution to the Lane-Emden equation using a polytropic fluid is known as a polytrope.

See also

• Adiabatic process
• Isentropic process
• Isobaric process
• Isochoric process
• Isothermal process
• vapor compression refrigeration
• gas compressor
• internal combustion engine
• Quasistatic equilibrium
• Thermodynamics