Polymatroid
In mathematics, polymatroid is a polytope associated with a submodular function. The notion was introduced by Jack Edmonds in 1970.[1]
Contents |
Definition
Consider any submodular set function  on
on  . Then define two associated polyhedra.
. Then define two associated polyhedra.
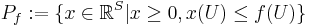 for each
for each 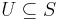
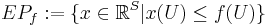 for each
for each 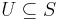
Here 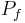 is called the polymatroid and
is called the polymatroid and 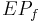 is called the extended polymatroid associated with
is called the extended polymatroid associated with  [2].
[2].
Properties
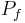 is nonempty if and only if
is nonempty if and only if 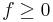 and that
and that 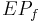 is nonempty if and only if
is nonempty if and only if 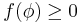
- Given any extended polymatroid
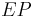 there is a unique submodular function
there is a unique submodular function  such that
such that  and
and 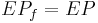
- If r is integral, 1-Lipschitz, and
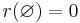 then r is the rank-function of a matroid, and the polymatroid is the independent set polytope, so-called since Edmonds showed it is the convex hull of the characteristic vectors of all independent sets of the matroid.
then r is the rank-function of a matroid, and the polymatroid is the independent set polytope, so-called since Edmonds showed it is the convex hull of the characteristic vectors of all independent sets of the matroid. - For a supermodular f one analogously may define the contrapolymatroid
-
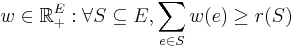
- This analogously generalizes the dominant of the spanning set polytope of matroids.
Citations
References
General References
- Schrijver, Alexander (2003), Combinatorial Optimization, Springer, ISBN 3540443894
- Lee, Jon (2004), A First Course in Combinatorial Optimization, Cambridge University Press, ISBN 0521010128
- Fujishige, Saruto (2005), Submodular Functions and Optimization, Elsevier, ISBN 0444520864
- Narayanan, H. (1997), Submodular Functions and Electrical Networks, ISBN 0444825231