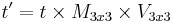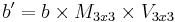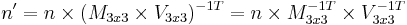Normal mapping
In 3D computer graphics, normal mapping, or "Dot3 bump mapping", is a technique used for faking the lighting of bumps and dents. It is used to add details without using more polygons. A common use of this technique is to greatly enhance the appearance and details of a low polygon model by generating a normal map from a high polygon model. Normal maps are frequently stored as RGB images where the RGB components corresponds to the X, Y, and Z coordinates, respectively, of the surface normal.
Contents |
History
The idea of taking geometric details from a high polygon model was introduced in "Fitting Smooth Surfaces to Dense Polygon Meshes" by Krishnamurthy and Levoy, Proc. SIGGRAPH 1996[1], where this approach was used for creating displacement maps over nurbs. In 1998, two papers were presented with key ideas for transferring details with normal maps from high to low polygon meshes: "Appearance Preserving Simplification", by Cohen et al. SIGGRAPH 1998[2], and "A general method for preserving attribute values on simplified meshes" by Cignoni et al. IEEE Visualization '98[3]. The former introduced the idea of storing surface normals directly in a texture, rather than displacements, though it required the low-detail model to be generated by a particular constrained simplification algorithm. The latter presented a simpler approach that decouples the high and low polygonal mesh and allows the recreation of any attributes of the high-detail model (color, texture coordinates, displacements, etc.) in a way that is not dependent on how the low-detail model was created. The combination of storing normals in a texture, with the more general creation process is still used by most currently available tools.
How it works
To calculate the Lambertian (diffuse) lighting of a surface, the unit vector from the shading point to the light source is dotted with the unit vector normal to that surface, and the result is the intensity of the light on that surface. Imagine a polygonal model of a sphere - you can only approximate the shape of the surface. By using a 3-channel bitmap textured across the model, more detailed normal vector information can be encoded. Each channel in the bitmap corresponds to a spatial dimension (X, Y and Z). These spatial dimensions are relative to a constant coordinate system for object-space normal maps, or to a smoothly varying coordinate system (based on the derivatives of position with respect to texture coordinates) in the case of tangent-space normal maps. This adds much more detail to the surface of a model, especially in conjunction with advanced lighting techniques.
Since a normal will be used in the dot product calculation for the diffuse lighting computation, we can see that the {0, 0, –1} would be remapped to the {128, 128, 255} values, giving that kind of sky blue color seen in normal maps (blue (z) coordinate is perspective (deepness) coordinate and RG-xy flat coordinates on screen). {0.3, 0.4, –0.866} would be remapped to the ({0.3, 0.4, –0.866}/2+{0.5, 0.5, 0.5})*255={0.15+0.5, 0.2+0.5, 0.433+0.5}*255={0.65, 0.7, 0.933}*255={166, 179, 238} values (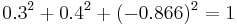 ). Coordinate z (blue) minus sign flipped, because need match normal map normal vector with eye (viewpoint or camera) vector or light vector (because sign "-" for z axis means vertex is in front of camera and not behind camera; when light vector and normal vector match surface shined with maximum strength).
). Coordinate z (blue) minus sign flipped, because need match normal map normal vector with eye (viewpoint or camera) vector or light vector (because sign "-" for z axis means vertex is in front of camera and not behind camera; when light vector and normal vector match surface shined with maximum strength).
Calculating Tangent Space
In order to find the perturbation in the normal the tangent space must be correctly calculated[4]. Most often the normal is perturbed in a fragment shader after applying the model and view matrices. Typically the geometry provides a normal and tangent. The tangent is part of the tangent plane and can be transformed simply with the linear part of the matrix (the upper 3x3). However, the normal needs to be transformed by the inverse transpose. Most applications will want cotangent to match the transformed geometry (and associated uv's). So instead of enforcing the cotangent to be perpendicular to the tangent, it is generally preferable to transform the cotangent just like the tangent. Let t be tangent, b be cotangent, n be normal, M3x3 be the linear part of model matrix, and V3x3 be the linear part of the view matrix.
Normal mapping in video games
Interactive normal map rendering was originally only possible on PixelFlow, a parallel rendering machine built at the University of North Carolina at Chapel Hill. It was later possible to perform normal mapping on high-end SGI workstations using multi-pass rendering and framebuffer operations[5] or on low end PC hardware with some tricks using paletted textures. However, with the advent of shaders in personal computers and game consoles, normal mapping became widely used in commercial video games starting in late 2003. Normal mapping's popularity for real-time rendering is due to its good quality to processing requirements ratio versus other methods of producing similar effects. Much of this efficiency is made possible by distance-indexed detail scaling, a technique which selectively decreases the detail of the normal map of a given texture (cf. mipmapping), meaning that more distant surfaces require less complex lighting simulation.
Basic normal mapping can be implemented in any hardware that supports palettized textures. The first game console to have specialized normal mapping hardware was the Sega Dreamcast. However, Microsoft's Xbox was the first console to widely use the effect in retail games. Out of the sixth generation consoles, only the PlayStation 2's GPU lacks built-in normal mapping support. Games for the Xbox 360 and the PlayStation 3 rely heavily on normal mapping and are beginning to implement parallax mapping. The Nintendo 3DS has been shown to support normal mapping, as demonstrated by Resident Evil Revelations and Metal Gear Solid: Snake Eater.
See also
References
- ^ Krishnamurthy and Levoy, Fitting Smooth Surfaces to Dense Polygon Meshes, SIGGRAPH 1996
- ^ Cohen et al., Appearance-Preserving Simplification, SIGGRAPH 1998 (PDF)
- ^ Cignoni et al., A general method for preserving attribute values on simplified meshes, IEEE Visualization 1998 (PDF)
- ^ Mikkelsen, Simulation of Wrinkled Surfaces Revisited, 2008 (PDF)
- ^ Heidrich and Seidel, Realistic, Hardware-accelerated Shading and Lighting, SIGGRAPH 1999 (PDF)
External links
- Understanding Normal Maps
- Introduction to Normal Mapping
- Blender Normal Mapping
- Normal Mapping with paletted textures using old OpenGL extensions.
- Normal Map Photography Creating normal maps manually by layering digital photographs
- Normal Mapping Explained
- xNormal A closed source, free normal mapper for Windows