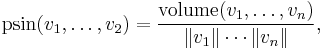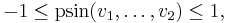Polar sine
In mathematics, the polar sine of a vertex angle of a polytope is defined as follows. Let v1, ..., vn, n ≥ 2, be non-zero vectors from the vertex in the directions of the edges. The polar sine of the vertex angle is
the volume in the numerator being that of the parallelotope whose edges at the vertex in question are the given vectors v1, ..., vn[1]. Also see Ericksson[2].
If the dimension of the space is more than n, then the polar sine is non-negative; otherwise it changes signs whenever two of the vectors are interchanged.
The absolute value of the polar sine does not change if all of the vectors v1, ..., vn are multiplied by positive constants. In case n = 2, the polar sine is the ordinary sine of the angle between the two vectors.
As for the ordinary sine, the polar sine is bounded by the inequalities
with either bound only being reached in case all vectors are mutually orthogonal.
Polar sines were investigated by Euler in the 18th century.[3]
References
- ^ Gilad Lerman and Tyler Whitehouse On d-dimensional d-semimetrics and simplex-type inequalities for high-dimensional sine functions
- ^ Eriksson, F. "The Law of Sines for Tetrahedra and n-Simplices." Geometriae Dedicata volume 7, pages 71–80, 1978.
- ^ Leonhard Euler, "De mensura angulorum solidorum", in Leonhardi Euleri Opera Omnia, volume 26, pages 204–223.
External links
- Weisstein, Eric W., "Polar Sine" from MathWorld.