Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate-transformations, the so-called "canonical transformations", which maps canonical coordinate systems into canonical coordinate systems. (A "canonical coordinate system" consists of canonical position/momentum variables, that satisfy canonical Poisson-bracket relations.) Note that the set of possible canonical transformations is always very rich. For instance, often it is possible to choose the Hamiltonian itself 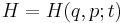 as one of the new canonical momentum coordinates.
as one of the new canonical momentum coordinates.
In a more general sense: the Poisson bracket is used to define a Poisson algebra, of which the algebra of functions on a Poisson manifold is a special case. These are all named in honour of Siméon-Denis Poisson.
Contents |
Canonical coordinates
In canonical coordinates (also known as Darboux coordinates) 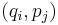 on the phase space, given two functions
on the phase space, given two functions 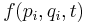 and
and 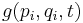 , the Poisson bracket takes the form
, the Poisson bracket takes the form
Hamilton's Equations of motion
The Hamilton's equations of motion have an equivalent expression in terms of the Poisson bracket. This may be most directly demonstrated in an explicit coordinate frame. Suppose that 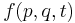 is a function on the manifold. Then one has
is a function on the manifold. Then one has
Then, by taking 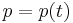 and
and 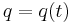 to be solutions to the Hamilton equations
to be solutions to the Hamilton equations 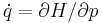 and
and 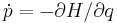 , one may write
, one may write
Thus, the time evolution of a function  on a symplectic manifold can be given as a one-parameter family of symplectomorphisms, with the time t being the parameter. Dropping the coordinates, one has
on a symplectic manifold can be given as a one-parameter family of symplectomorphisms, with the time t being the parameter. Dropping the coordinates, one has
The operator 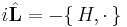 is known as the Liouvillian.
is known as the Liouvillian.
Constants of motion
An integrable dynamical system will have constants of motion in addition to the energy. Such constants of motion will commute with the Hamiltonian under the Poisson bracket. Suppose some function 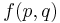 is a constant of motion. This implies that if
is a constant of motion. This implies that if 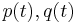 is a trajectory or solution to the Hamilton's equations of motion, then one has that
is a trajectory or solution to the Hamilton's equations of motion, then one has that 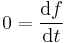 along that trajectory. Then one has
along that trajectory. Then one has
where, as above, the intermediate step follows by applying the equations of motion. This equation is known as the Liouville equation. The content of Liouville's theorem is that the time evolution of a measure (or "distribution function" on the phase space) is given by the above.
In order for a Hamiltonian system to be completely integrable, all of the constants of motion must be in mutual involution.
Definition
Let M be symplectic manifold, that is, a manifold equipped with a symplectic form: a 2-form  which is both closed (
which is both closed (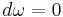 ) and non-degenerate, in the following sense: when viewed as a map
) and non-degenerate, in the following sense: when viewed as a map ![\ \omega: \xi \in \mathrm{vect}[M] \rightarrow i_\xi \omega \in \Lambda^1[M]](/2012-wikipedia_en_all_nopic_01_2012/I/f9f0de581b43c7d44b2ac7f446f87611.png) ,
, 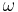 is invertible to obtain
is invertible to obtain ![\tilde{\omega}: \Lambda^1[M] \rightarrow \mathrm{vect}[M]](/2012-wikipedia_en_all_nopic_01_2012/I/e9ff0e93ef833677ab232b4a6ba10bdc.png) . Here
. Here 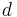 is the exterior derivative operation intrinsic to the manifold structure of M, and
is the exterior derivative operation intrinsic to the manifold structure of M, and 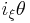 is the interior product or contraction operation, which is equivalent to
is the interior product or contraction operation, which is equivalent to 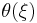 on 1-forms
on 1-forms 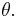
Using the axioms of the exterior calculus, one can derive:
Here ![\ [v, w]](/2012-wikipedia_en_all_nopic_01_2012/I/60c07e93a0c53df4c7dde20c1f91efa6.png) denotes the Lie bracket on smooth vector fields, whose properties essentially define the manifold structure of M.
denotes the Lie bracket on smooth vector fields, whose properties essentially define the manifold structure of M.
If v is such that 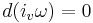 , we may call it
, we may call it  -coclosed (or just coclosed). Similarly, if
-coclosed (or just coclosed). Similarly, if 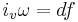 for some function f, we may call v
for some function f, we may call v  -coexact (or just coexact). Given that
-coexact (or just coexact). Given that 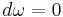 , the expression above implies that the Lie bracket of two coclosed vector fields is always a coexact vector field, because when v and w are both coclosed, the only nonzero term in the expression is
, the expression above implies that the Lie bracket of two coclosed vector fields is always a coexact vector field, because when v and w are both coclosed, the only nonzero term in the expression is 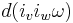 . And because the exterior derivative obeys
. And because the exterior derivative obeys 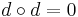 , all coexact vector fields are coclosed; so the Lie bracket is closed both on the space of coclosed vector fields and on the subspace within it consisting of the coexact vector fields. In the language of abstract algebra, the coclosed vector fields form a subalgebra of the Lie algebra of smooth vector fields on M, and the coexact vector fields form an algebraic ideal of this subalgebra.
, all coexact vector fields are coclosed; so the Lie bracket is closed both on the space of coclosed vector fields and on the subspace within it consisting of the coexact vector fields. In the language of abstract algebra, the coclosed vector fields form a subalgebra of the Lie algebra of smooth vector fields on M, and the coexact vector fields form an algebraic ideal of this subalgebra.
Given the existence of the inverse map 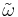 , every smooth real-valued function f on M may be associated with a coexact vector field
, every smooth real-valued function f on M may be associated with a coexact vector field 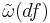 . (Two functions are associated with the same vector field if and only if their difference is in the kernel of d, i. e., constant on each connected component of M.) We therefore define the Poisson bracket on
. (Two functions are associated with the same vector field if and only if their difference is in the kernel of d, i. e., constant on each connected component of M.) We therefore define the Poisson bracket on 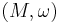 , a bilinear operation on differentiable functions, under which the
, a bilinear operation on differentiable functions, under which the 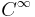 (smooth) functions form an algebra. It is given by:
(smooth) functions form an algebra. It is given by:
The skew-symmetry of the Poisson bracket is ensured by the axioms of the exterior calculus and the condition 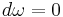 . Because the map
. Because the map 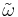 is pointwise linear and skew-symmetric in this sense, some authors associate it with a bivector, which is not an object often encountered in the exterior calculus. In this form it is called the Poisson bivector or the Poisson structure on the symplectic manifold, and the Poisson bracket written simply
is pointwise linear and skew-symmetric in this sense, some authors associate it with a bivector, which is not an object often encountered in the exterior calculus. In this form it is called the Poisson bivector or the Poisson structure on the symplectic manifold, and the Poisson bracket written simply 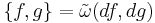 .
.
The Poisson bracket on smooth functions corresponds to the Lie bracket on coexact vector fields and inherits its properties. It therefore satisfies the Jacobi identity:
The Poisson bracket 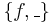 with respect to a particular scalar field f corresponds to the Lie derivative with respect to
with respect to a particular scalar field f corresponds to the Lie derivative with respect to 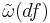 . Consequently, it is a derivation; that is, it satisfies Leibniz' law:
. Consequently, it is a derivation; that is, it satisfies Leibniz' law:
also known as the "Poisson property". It is a fundamental property of manifolds that the commutator of the Lie derivative operations with respect to two vector fields is equivalent to the Lie derivative with respect to some vector field, namely, their Lie bracket. The parallel role of the Poisson bracket is apparent from a rearrangement of the Jacobi identity:
If the Poisson bracket of f and g vanishes (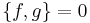 ), then f and g are said to be in mutual involution, and the operations of taking the Poisson bracket with respect to f and with respect to g commute.
), then f and g are said to be in mutual involution, and the operations of taking the Poisson bracket with respect to f and with respect to g commute.
Lie algebra
The Poisson bracket is skewsymmetric/antisymmetric. (Equivalently, viewed as a binary product operation, it is anticommutative.) It also satisfies the Jacobi identity. This makes the space of smooth functions on a symplectic manifold an infinite-dimensional Lie algebra with the Poisson bracket acting as the Lie bracket. The corresponding Lie group is the group of symplectomorphisms of the symplectic manifold (also known as canonical transformations).
Given a smooth vector field X on the tangent bundle, let 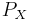 be its conjugate momentum. The conjugate momentum mapping is a Lie algebra anti-homomorphism from the Poisson bracket to the Lie bracket:
be its conjugate momentum. The conjugate momentum mapping is a Lie algebra anti-homomorphism from the Poisson bracket to the Lie bracket:
This important result is worth a short proof. Write a vector field X at point q in the configuration space as
where the 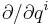 is the local coordinate frame. The conjugate momentum to X has the expression
is the local coordinate frame. The conjugate momentum to X has the expression
where the 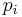 are the momentum functions conjugate to the coordinates. One then has, for a point
are the momentum functions conjugate to the coordinates. One then has, for a point 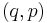 in the phase space,
in the phase space,
The above holds for all 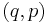 , giving the desired result.
, giving the desired result.
See also
- Poisson algebra
- Phase space
- Lagrange bracket
- Moyal bracket
- Peierls bracket
- Poisson superalgebra
- Poisson superbracket
- Dirac bracket
- Commutator
References
- Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics (2nd ed. ed.). New York: Springer. ISBN 978-0387968902.
- Landau, L. D.; Lifshitz, E. M. (1982). Mechanics. Course of Theoretical Physics. Vol. 1 (3rd ed. ed.). Butterworth-Heinemann. ISBN 978-0750628969.
- Karasëv, M. V.; Maslov, V. P.: Nonlinear Poisson brackets. Geometry and quantization. Translated from the Russian by A. Sossinsky [A. B. Sosinskiĭ] and M. Shishkova. Translations of Mathematical Monographs, 119. American Mathematical Society, Providence, RI, 1993.
![\{f,g\} = \sum_{i=1}^{N} \left[
\frac{\partial f}{\partial q_{i}} \frac{\partial g}{\partial p_{i}} -
\frac{\partial f}{\partial p_{i}} \frac{\partial g}{\partial q_{i}}
\right].](/2012-wikipedia_en_all_nopic_01_2012/I/8bb83f8303c20e0c2436ddd07abe132d.png)
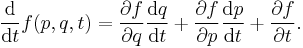
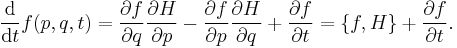
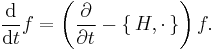
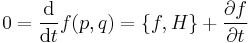
![\ i_{[v, w]} \omega = d(i_v i_w \omega) %2B i_v d(i_w \omega) - i_w d(i_v \omega) - i_w i_v d\omega.](/2012-wikipedia_en_all_nopic_01_2012/I/00944af7bfd4a4cbe8f39ac82ff86375.png)
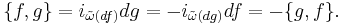
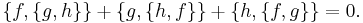
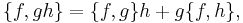
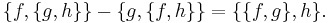
![\{P_X,P_Y\}=-P_{[X,Y]}.\,](/2012-wikipedia_en_all_nopic_01_2012/I/53a18960c0b08fc9a6d356efe3bd71c5.png)
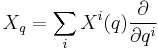
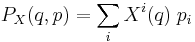
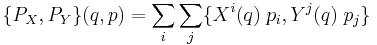
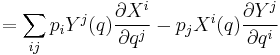
![= - \sum_i p_i \; [X,Y]^i(q)](/2012-wikipedia_en_all_nopic_01_2012/I/0791d653f917960fe59c04b1bbd549ad.png)
![= - P_{[X,Y]}(q,p). \,](/2012-wikipedia_en_all_nopic_01_2012/I/f19e0ab6d80bbea66155331a4c9f6967.png)