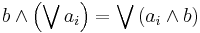Pointless topology
In mathematics, pointless topology (also called point-free or pointfree topology) is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann.[1] The ideas of pointless topology are closely related to mereotopologies in which regions (sets) are treated as foundational without explicit reference to underlying point sets.
Contents |
General concepts
Traditionally, a topological space consists of a set of points, together with a system of open sets. These open sets with the operations of intersection and union form a lattice with certain properties. Pointless topology then studies lattices like these abstractly, without reference to any underlying set of points. Since some of the so-defined lattices do not arise from topological spaces, one may see the category of pointless topological spaces, also called locales, as an extension of the category of ordinary topological spaces.
Categories of frames and locales
Formally, a frame is defined to be a lattice L in which finite meets distribute over arbitrary joins, i.e. every (even infinite) subset {ai} of L has a supremum ⋁ai such that
for all b in L. These frames, together with lattice homomorphisms that respect arbitrary suprema, form a category. The dual of the category of frames is called the category of locales and generalizes the category Top of all topological spaces with continuous functions. The consideration of the dual category is motivated by the fact that every continuous map between topological spaces X and Y induces a map between the lattices of open sets in the opposite direction as for every continuous function f: X → Y and every open set O in Y the inverse image f -1(O) is an open set in X.
Relation to point-set topology
It is possible to translate most concepts of point-set topology into the context of locales, and prove analogous theorems. While many important theorems in point-set topology require the axiom of choice, this is not true for some of their analogues in locale theory. This can be useful if one works in a topos that does not have the axiom of choice.
The concept of "product of locales" diverges slightly from the concept of "product of topological spaces", and this divergence has been called a disadvantage of the locale approach. Others claim that the locale product is more natural, and point to several "desirable" properties not shared by products of topological spaces.
For almost all spaces (more precisely for sober spaces), the topological product and the localic product have the same set of points. The products differ in how equality between sets of open rectangles, the canonical base for the product topology, is defined: equality for the topological product means the same set of points is covered; equality for the localic product means provable equality using the frame axioms. As a result, two open sublocales of a localic product may contain exactly the same points without being equal.
A point where locale theory and topology diverge much more strongly is the concept of subspaces vs. sublocales. The rational numbers have c subspaces but 2c sublocales. The proof for the latter statement is due to John Isbell, and uses the fact that the rational numbers have c many pairwise almost disjoint (= finite intersection) closed subspaces.
See also
- Heyting algebra. A locale is a complete Heyting algebra.
- Details on the relationship between the category of topological spaces and the category of locales, including the explicit construction of the duality between sober spaces and spatial locales, are to be found in the article on Stone duality.
- Point-free geometry
- Mereology
- Mereotopology
- Tacit programming
References
- ^ Garrett Birkhoff, VON NEUMANN AND LATTICE THEORY, John Von Neumann 1903-1957, J. C. Oxtoley, B. J. Pettis, American Mathematical Soc., 1958, page 50-5
- Johnstone, Peter T., 1983, "The point of pointless topology," Bulletin of the American Mathematical Society 8(1): 41-53.