Point process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces. For example, the occurrence of lightning strikes might be considered as a point process in both time and geographical space if each is recorded according to its location in time and space.
Point processes are well studied objects in probability theory[1][2] and the subject of powerful tools in statistics for modeling and analyzing spatial data,[3][4] which is of interest in such diverse disciplines as forestry, plant ecology, epidemiology, geography, seismology, materials science, astronomy, telecommunications, economics[5] and others.
Point processes on the real line form an important special case that is particularly amenable to study,[6] because the different points are ordered in a natural way, and the whole point process can be described completely by the (random) intervals between the points. These point processes are frequently used as models for random events in time, such as the arrival of customers in a queue (queueing theory), of impulses in a neuron (computational neuroscience), particles in a Geiger counter, location of radio stations in a telecommunication network[7] or of searches on the world-wide web.
Contents |
General point process theory
In mathematics, a point process is a random element whose values are "point patterns" on a set S. While in the exact mathematical definition a point pattern is specified as a locally finite counting measure, it is sufficient for more applied purposes to think of a point pattern as a countable subset of S that has no limit points.
Definition
Let S be locally compact second countable Hausdorff space equipped with its Borel σ-algebra B(S). Write 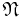 for the set of locally finite counting measures on S and
for the set of locally finite counting measures on S and 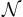 for the smallest σ-algebra on
for the smallest σ-algebra on 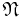 that renders all the point counts
that renders all the point counts
for relatively compact sets B in B measurable.
A point process on S is a measurable map
from a probability space 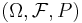 to the measurable space
to the measurable space 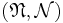 .
.
By this definition, a point process is a special case of a random measure.
The most common example for the state space S is the Euclidean space Rn or a subset thereof, where a particularly interesting special case is given by the real half-line [0,∞). However, point processes are not limited to these examples and may among other things also be used if the points are themselves compact subsets of Rn, in which case ξ is usually referred to as a particle process.
It has been noted that the term point process is not a very good one if S is not a subset of the real line, as it might suggest that ξ is a stochastic process. However, the term is well established and uncontested even in the general case.
Representation
Every point process ξ can be represented as
where  denotes the Dirac measure, N is a integer-valued random variable and
denotes the Dirac measure, N is a integer-valued random variable and 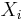 are random elements of S. If
are random elements of S. If 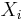 's are almost surely distinct (or equivalently, almost surely
's are almost surely distinct (or equivalently, almost surely 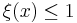 for all
for all 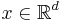 ), then the point process is known as simple.
), then the point process is known as simple.
Expectation measure
The expectation measure Eξ (also known as mean measure) of a point process ξ is a measure on S that assigns to every Borel subset B of S the expected number of points of ξ in B. That is,
Laplace functional
The Laplace functional 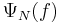 of a point process N is a map from the set of all positive valued functions f on the state space of N, to
of a point process N is a map from the set of all positive valued functions f on the state space of N, to 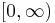 defined as follows:
defined as follows:
They play a similar role as the characteristic functions for random variable. One important theorem says that: two point processes have the same law iff their Laplace functionals are equal.
Moment measures
The  th power of a point process,
th power of a point process, 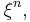 is defined on the product space
is defined on the product space 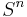 as follows :
as follows :
By monotone class theorem, this uniquely defines the product measure on 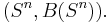 The expectation
The expectation 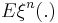 is called the
is called the  th moment measure. The first moment measure is the mean measure.
th moment measure. The first moment measure is the mean measure.
Let 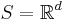 . The joint intensities of a point process
. The joint intensities of a point process 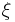 w.r.t. the Lebesgue measure are functions
w.r.t. the Lebesgue measure are functions 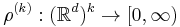 such that for any disjoint bounded Borel subsets
such that for any disjoint bounded Borel subsets 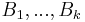
Joint intensities do not always exist for point processes. Given that moments of a random variable determine the random variable in many cases, a similar result is to be expected for joint intensities. Indeed, this has been shown in many cases.[2]
Stationarity
A point process 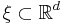 is said to be stationary if
is said to be stationary if 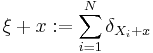 has the same distribution as
has the same distribution as 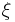 for all
for all 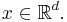 For a stationary point process, the mean measure
For a stationary point process, the mean measure  for some constant
for some constant 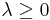 and where
and where  stands for the Lebesgue measure. This
stands for the Lebesgue measure. This  is called the intensity of the point process. A stationary point process on
is called the intensity of the point process. A stationary point process on 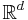 has almost surely either 0 or an infinite number of points in total. For more on stationary point processes and random measure, refer to Chapter 12 of Daley & Vere-Jones.[2] It is to be noted that stationarity has been defined and studied for point processes in more general spaces than
has almost surely either 0 or an infinite number of points in total. For more on stationary point processes and random measure, refer to Chapter 12 of Daley & Vere-Jones.[2] It is to be noted that stationarity has been defined and studied for point processes in more general spaces than 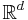 .
.
Examples of point processes
We shall see some examples of point processes in 
Poisson point process
The simplest and ubiquitous example of a point process is the Poisson point process, which is a spatial generalisation of the Poisson process. A Poisson process on the line can be characterised by two properties : the number of points (or events) in disjoint intervals are independent and have a Poisson distribution. A Poisson point process can also be defined using these two properties. Namely, we say that a point process 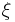 is a Poisson point process if the following two conditions hold
is a Poisson point process if the following two conditions hold
1) 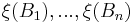 are independent for disjoint subsets
are independent for disjoint subsets 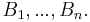
2) For any bounded subset  ,
, 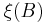 has a Poisson distribution with parameter
has a Poisson distribution with parameter 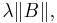 where
where  denotes the Lebesgue measure.
denotes the Lebesgue measure.
The two conditions can be combined together and written as follows : For any disjoint bounded subsets 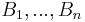 and non-negative integers
and non-negative integers 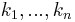 we have that
we have that
The constant  is called the intensity of the Poisson point process. Note that the Poisson point process is characterised by the single parameter
is called the intensity of the Poisson point process. Note that the Poisson point process is characterised by the single parameter 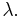 It is a simple, stationary point process. To be more specific one calls the above point process, an homogeneous Poisson point process. An inhomogeneous Poisson point process is defined as above but by replacing
It is a simple, stationary point process. To be more specific one calls the above point process, an homogeneous Poisson point process. An inhomogeneous Poisson point process is defined as above but by replacing 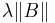 with
with 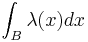 where
where  is a non-negative function on
is a non-negative function on 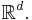
Cox point process
This class of point processes are named after Sir David Cox. These generalise the Poisson point process in that we use random measures in place of 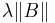 . More formally, let
. More formally, let 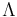 be a random measure. A Cox point process driven by the random measure
be a random measure. A Cox point process driven by the random measure 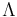 is the point process
is the point process 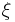 with the following two properties :
with the following two properties :
- Given
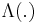 ,
, 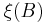 is Poisson distributed with parameter
is Poisson distributed with parameter 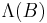 for any bounded subset
for any bounded subset 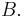
- For any finite collection of disjoint subsets
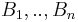 and conditioned on
and conditioned on 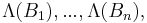 we have that
we have that 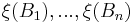 are independent.
are independent.
It is easy to see that Poisson point process (homogeneous and inhomogeneous) follow as special cases of Cox point processes. The mean measure of a Cox point process is  and thus in the special case of a Poisson point process, it is
and thus in the special case of a Poisson point process, it is 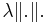
For a Cox point process, 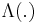 is called the intensity measure. Further, if
is called the intensity measure. Further, if 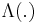 has a (random) density (Radon-Nikodyn derivative)
has a (random) density (Radon-Nikodyn derivative) 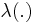 i.e.,
i.e.,
then 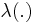 is called the intensity field of the Cox point process. Stationarity of the intensity measures or intensity fields imply the stationarity of the corresponding Cox point processes.
is called the intensity field of the Cox point process. Stationarity of the intensity measures or intensity fields imply the stationarity of the corresponding Cox point processes.
There have been many specific classes of Cox point processes that have been studied in detail such as:
- Log Gaussian Cox point processes:[8]
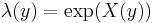 for a Gaussian random field
for a Gaussian random field 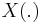
- Shot noise Cox point processes:,[9]
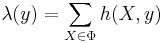 for a Poisson point process
for a Poisson point process 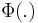 and kernel
and kernel 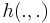
- Generalised shot noise Cox point processes:[10]
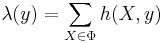 for a point process
for a point process 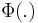 and kernel
and kernel 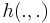
- Lévy based Cox point processes:[11]
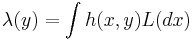 for a Lévy basis
for a Lévy basis 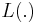 and kernel
and kernel 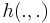 , and
, and - Permanental Cox point processes:[12]
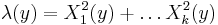 for k independent Gaussian random fields
for k independent Gaussian random fields 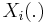 's
's - Sigmoidal Gaussian Cox point processes:[13]
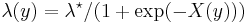 for a Gaussian random field
for a Gaussian random field 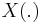 and random
and random 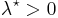
By Jensen's inequality, one can verify that Cox point processes satisfy the following inequality: for all bounded Borel subsets  ,
,
where 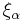 stands for a Poisson point process with intensity measure
stands for a Poisson point process with intensity measure 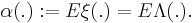 Thus points are distributed with greater variability in a Cox point process compared to a Poisson point process. This is sometimes called clustering or attractive property of the Cox point process.
Thus points are distributed with greater variability in a Cox point process compared to a Poisson point process. This is sometimes called clustering or attractive property of the Cox point process.
Determinantal point processes
An important class of point processes, with applications to physics, random matrix theory, and combinatorics, is that of determinantal point processes.
Point processes on the real half-line
Historically the first point processes that were studied had the real half line R+ = [0,∞) as their state space, which in this context is usually interpreted as time. These studies were motivated by the wish to model telecommunication systems,[14] in which the points represented events in time, such as calls to a telephone exchange.
Point processes on R+ are typically described by giving the sequence of their (random) inter-event times (T1, T2,...), from which the actual sequence (X1, X2,...) of event times can be obtained as
If the inter-event times are independent and identically distributed, the point process obtained is called a renewal process.
Conditional intensity function
The conditional intensity function of a point process on the real half-line is a function λ(t|Ht) defined as
where Ht denotes the history of event times preceding time t.
Papangelou intensity function
The Papangelou intensity function of a point process  in the
in the  -dimensional Euclidean space
-dimensional Euclidean space 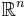 is defined as:
is defined as:
![\lambda_p(x)=\lim_{\delta \to 0}\frac{1}{|B_\delta (x)|}{P}\{\mbox{One event occurs in } \,B_\delta(x)\,|\, \sigma[N \setminus(B_\delta(x))] \} ,](/2012-wikipedia_en_all_nopic_01_2012/I/f3b86d58e9236ed051ea4baeb427effa.png)
where 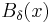 is the ball centered at
is the ball centered at  of a radius
of a radius  , and
, and ![\sigma[N \setminus(B_\delta(x))]](/2012-wikipedia_en_all_nopic_01_2012/I/8d542fa6977f23c7bc2c20fb4f67e1bd.png) denotes the information of the point process
denotes the information of the point process  outside
outside 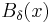 .
.
Point processes in spatial statistics
The analysis of point pattern data in a compact subset S of Rn is a major object of study within spatial statistics. Such data appear in a broad range of disciplines,[15] amongst which are
- forestry and plant ecology (positions of trees or plants in general)
- epidemiology (home locations of infected patients)
- zoology (burrows or nests of animals)
- geography (positions of human settlements, towns or cities)
- seismology (epicenters of earthquakes)
- materials science (positions of defects in industrial materials)
- astronomy (locations of stars or galaxies)
- computational neuroscience (spikes of neurons).
The need to use point processes to model these kinds of data lies in their inherent spatial structure. Accordingly, a first question of interest is often whether the given data exhibit complete spatial randomness (i.e. are a realization of a spatial Poisson process) as opposed to exhibiting either spatial aggregation or spatial inhibition.
In contrast, many datasets considered in classical multivariate statistics consist of indepently generated datapoints that may be governed by one or several covariates (typically non-spatial).
Apart from the applications in spatial statistics, point processes are one of the fundamental objects in stochastic geometry. Research has also focussed extensively on various models built on point processes such as Voronoi Tessellations, Random geometric graphs, Boolean model etc.
See also
References
- ^ Kallenberg, O. (1986). Random Measures, 4th edition. Academic Press, New York, London; Akademie-Verlag, Berlin. ISBN 0-123-94960-2, MR854102.
- ^ a b c Daley, D.J, Vere-Jones, D. (1988). An Introduction to the Theory of Point Processes. Springer, New York. ISBN 0-387-96666-8, MR950166.
- ^ Diggle, P. (2003). Statistical Analysis of Spatial Point Patterns, 2nd edition. Arnold, London. ISBN 0-340-74070-1.
- ^ Baddeley, A. (2006). Spatial point processes and their applications. In A. Baddeley, I. Bárány, R. Schneider, and W. Weil, editors, Stochastic Geometry: Lectures given at the C.I.M.E. Summer School held in Martina Franca, Italy, September 13–18, 2004, Lecture Notes in Mathematics 1892, Springer. ISBN 3-540-38174-0, pp. 1--75
- ^ Robert F. Engle and Asger Lunde, 2003, "Trades and Quotes: A Bivariate Point Process". Journal of Financial Econometrics Vol. 1, No. 2, pp. 159-188
- ^ Last, G., Brandt, A. (1995).Marked point processes on the real line: The dynamic approach. Probability and its Applications. Springer, New York. ISBN 0-387-94547-4, MR1353912
- ^ Gilbert, E.N. (1961) Random plane networks. SIAM Journal, Vol. 9, No. 4.
- ^ Moller, J.; Syversveen, A. R.; Waagepetersen, R. P. (1998). "Log Gaussian Cox Processes". Scandinavian Journal of Statistics 25 (3): 451. doi:10.1111/1467-9469.00115.
- ^ Moller, J. (2003) Shot noise Cox processes, Adv. Appl. Prob., 35.
- ^ Moller, J. and Torrisi, G.L. (2005) "Generalised Shot noise Cox processes", Adv. Appl. Prob., 37.
- ^ Hellmund, G., Prokesova, M. and Vedel Jensen, E.B. (2008) "Lévy-based Cox point processes", Adv. Appl. Prob., 40.
- ^ Mccullagh,P. and Moller, J. (2006) "The permanental processes", Adv. Appl. Prob., 38.
- ^ Adams, R.P., Murray, I. MacKay, D.J.C. (2009) "Tractable inference in Poisson processes with Gaussian process intensities", Proceedings of the 26th International Conference on Machine Learning doi:10.1145/1553374.1553376
- ^ Palm, C. (1943). Intensitätsschwankungen im Fernsprechverkehr (German). Ericsson Technics no. 44, (1943).MR11402
- ^ Baddeley, A., Gregori, P., Mateu, J., Stoica, R., and Stoyan, D., editors (2006). Case Studies in Spatial Point Pattern Modelling, Lecture Notes in Statistics No. 185. Springer, New York. ISBN 0-387-28311-0.
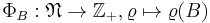
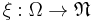
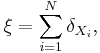
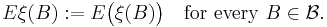
![\Psi_{N}(f)=E[\exp(-N(f))]](/2012-wikipedia_en_all_nopic_01_2012/I/754ed9fd0368587e87171488061cff1d.png)
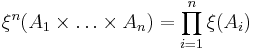
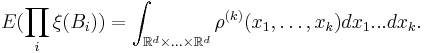
![Pr[\xi(B_i) = k_i, 1 \leq i \leq n] = \prod_i e^{-\lambda \|B_i\|}\frac{(\lambda \|B_i\|)^{k_i}}{k_i!}.](/2012-wikipedia_en_all_nopic_01_2012/I/df1ec6236b596494ccf0f29878d5ce52.png)
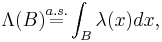
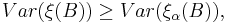
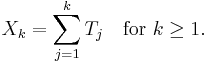
![\lambda(t| H_{t})=\lim_{\Delta t\to 0}\frac{1}{\Delta t}{P}(\mbox{One event occurs in the time-interval}\,[t,t%2B\Delta t]\,|\, H_t) ,](/2012-wikipedia_en_all_nopic_01_2012/I/002e7973ab05813c25b034cd0bdbbddf.png)