Poincaré–Steklov operator
In mathematics, a Poincaré–Steklov operator (after Henri Poincaré and Vladimir Steklov) maps the values of one boundary condition of the solution of an elliptic partial differential equation in a domain to the values of another boundary condition. Usually, either of the boundary conditions determines the solution. Thus, a Poincaré–Steklov operator encapsulates the boundary response of the system modelled by the partial differential equation. When the partial differential equation is discretized, for example by finite elements or finite differences, the discretization of the Poincaré–Steklov operator is the Schur complement obtained by eliminating all degrees of freedom inside the domain.
Note that there may be many suitable different boundary conditions for a given partial differential equation and the direction in which a Poincaré–Steklov operator maps the values of one into another is given only by a convention.[1]
Contents |
Dirichlet-to-Neumann operator on a bounded domain
Consider a steady-state distribution of temperature in a body for given temperature values on the body surface. Then the resulting heat flux through the boundary (that is, the heat flux that would be required to maintain the given surface temperature) is determined uniquely. The mapping of the surface temperature to the surface heat flux is a Poincaré–Steklov operator. This particular Poincaré–Steklov operator is called the Dirichlet to Neumann (DtN) operator. The values of the temperature on the surface is the Dirichlet boundary condition of the Laplace equation, which describes the distribution of the temperature inside the body. The heat flux through the surface is the Neumann boundary condition (proportional to the normal derivative of the temperature).
Mathematically, for a function  harmonic in a domain
harmonic in a domain 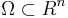 , the Dirichlet-to-Neumann operator maps the values of
, the Dirichlet-to-Neumann operator maps the values of  on the boundary of
on the boundary of  to the normal derivative
to the normal derivative 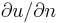 on the boundary of
on the boundary of  . This Poincaré–Steklov operator is at the foundation of iterative substructuring.[2]
. This Poincaré–Steklov operator is at the foundation of iterative substructuring.[2]
Dirichlet-to-Neumann operator for a boundary condition at infinity
The solution of partial differential equation in an external domain gives rise to a Poincaré–Steklov operator that brings the boundary condition from infinity to the boundary. One example is the Dirichlet-to-Neumann operator that maps the given temperature on the boundary of a cavity in infinite medium with zero temperature at infinity to the heat flux on the cavity boundary. Similarly, one can define the Dirichlet-to-Neumann operator on the boundary of a sphere for the solution for the Helmholtz equation in the exterior of the sphere. Approximations of this operator are at the foundation of a class of method for the modeling of acoustic scattering in infinite medium, with the scatterer enclosed in the sphere and the Poincaré–Steklov operator serving as a non-reflective (or absorbing) boundary condition.[3]
Poincaré–Steklov operator in electromagnetics
Here, the Poincaré–Steklov operator is defined to be the operator mapping the time-harmonic (that is, dependent on time as 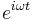 ) tangential electric field on the boundary of a conductive body to the electric current through the boundary.[4]
) tangential electric field on the boundary of a conductive body to the electric current through the boundary.[4]
See also
- Fluid-structure interaction (boundary/interface) analysis
- Schur complement domain decomposition method
References
- Lebedev, V. I.; Agoshkov, V. I. Operatory Puankare-Steklova i ikh prilozheniya v analize. (Russian) [Poincaré Steklov operators and their applications in analysis] Akad. Nauk SSSR, Vychisl. Tsentr, Moscow, 1983. 184 pp. MR87i:35053
- Vassilevski, P. S. Poincaré–Steklov operators for elliptic difference problems. C. R. Acad. Bulgare Sci. 38 (1985), no. 5, 543—546. MR86k:39007
- ^ A. Bossavit, The "scalar" Poincaré–Steklov operator and the "vector" one: algebraic structures which underlie their duality. In Fourth International Symposium on Domain Decomposition Methods for Partial Differential Equations (Moscow, 1990), pages 19–26. SIAM, Philadelphia, PA, 1991.
- ^ Alfio Quarteroni and Alberto Valli, Domain Decomposition Methods for Partial Differential Equations, Oxford Science Publications, 1999
- ^ Assad A. Oberai, Manish Malhotra, and Peter M. Pinsky, On the implementation of the Dirichlet-to-Neumann radiation condition for iterative solution of the Helmholtz equation. Appl. Numer. Math., 27(4):443–464, 1998.
- ^ L. F. Knockaert, On the complex symmetry of the Dirichlet-to-Neumann operator, Progress in Electromagnetics Research B, Vol. 7, 145–157, 2008. doi:10.2528/PIERB08022102
|
|||||||||||||||||